| |
|
| 阅读网 -> 人物音乐 -> 为什么有很多“不可能三角”,却很少听人说到“不可能四角”或者“不可能五角”? -> 正文阅读 |
|
|
[人物音乐]为什么有很多“不可能三角”,却很少听人说到“不可能四角”或者“不可能五角”? |
| [收藏本文] 【下载本文】 |
|
为什么有很多“不可能三角”,却很少听人说到“不可能四角”或者“不可能五角”? 关注问题?写回答 [img_log] [img_log] 不可能三角 为什么有很多“不可能三角”,却很少听人说到“不可能四角”或者“不可能五角”? |
|
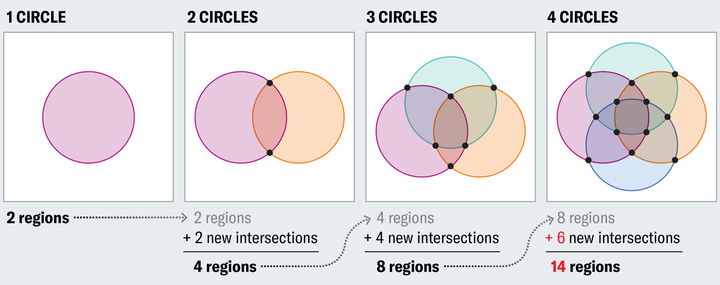
我感觉主要是不好画,你知道四元素韦恩图怎么画吗? 三元好画好理解,中间那个就是不存在。 如果你沿着三元素的思路画四元素,然后把中间的标记为不存在,那么会有个问题,这并不包含所有元素的交。 |
|
|
你没法表示 AC 的交和 BD 的交,也就是没法表达两种对立元素同时拥有的情况。 |
|
|
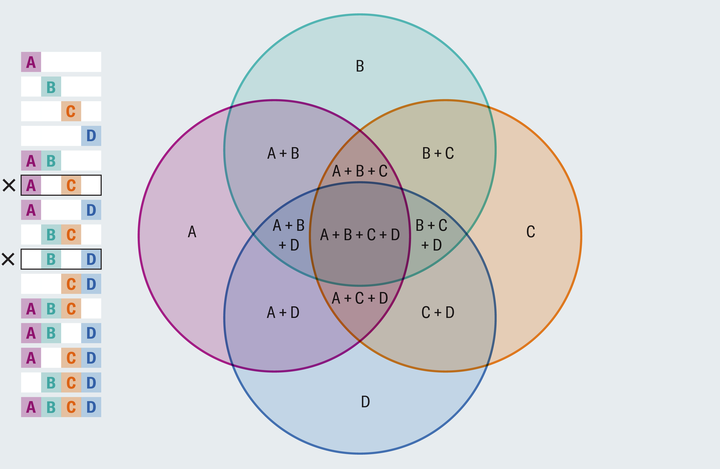
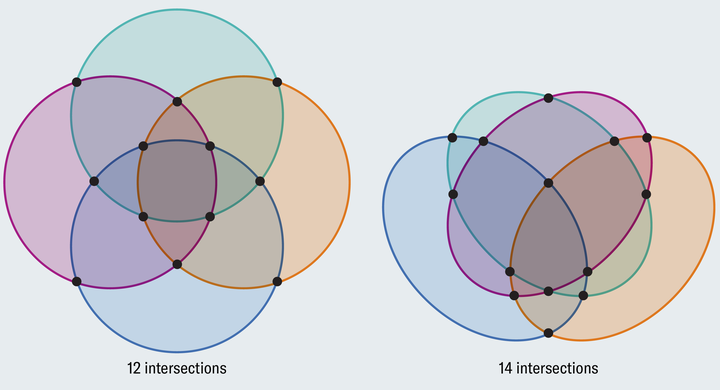
正确的画法如右图,这东西才能表达所有元素的交,然后再分类讨论不可能同时拥有的四个元素的排列组合。 |
|
|
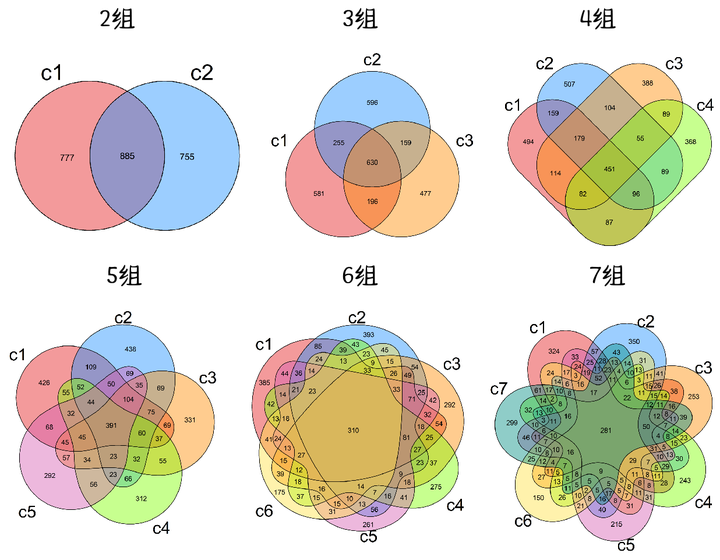
然后可以编一个编程不可能四角: 极致性能:运行速度极快,延迟低,吞吐量高,资源占用少。简洁优雅:代码逻辑清晰,易于理解和维护,菜鸡能快速上手,开发和迭代速度快。绝对可靠:在任何情况下都能正确运行,没有 bug,能抵御错误输入和外部系统故障,具备极高的稳定性和安全性。高度灵活:易于扩展和修改,能够轻松适应未来的需求变化,模块化程度高,可配置性强。 五元素就更复杂了,得画成灯泡形状,而且排列组合数量也太多了点,分类讨论脑子要炸了。 |
|
|
送礼物 还没有人送礼物,鼓励一下作者吧 |
|
因为不能“面面俱到”是司空见惯的现象,所以,“不可能四角”,“不可能五角”并不能引起人们的兴趣。 而对立的事物也很常见,所以“不可能两极”也不是什么特别现象。因此最多见的就是“不可能三角”。 送礼物 还没有人送礼物,鼓励一下作者吧 |
|
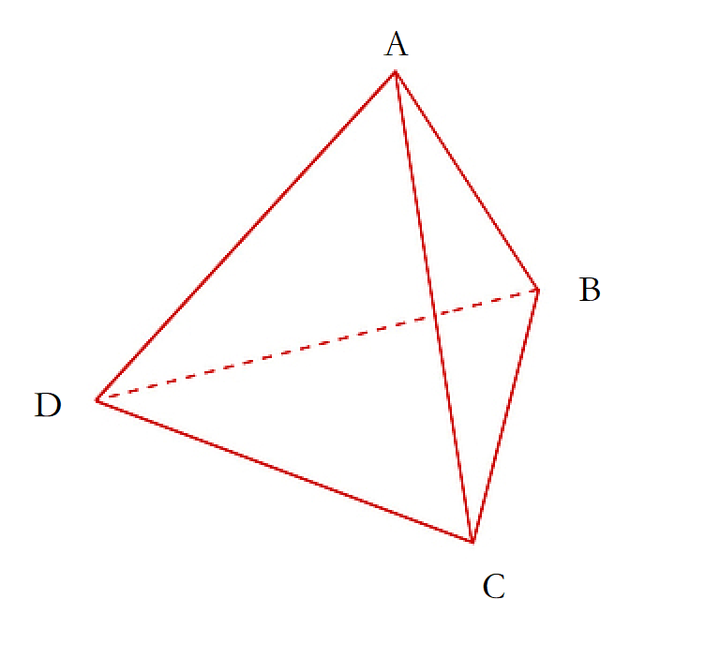
这不是几何或者数学问题,是媒体传播社会学问题。 要表达“不可能四角”很简单,一个四面体就可以,想表达任何三个条件可以同时满足,但不能满足四个条件,那就是随机取三点必然共面,但第四点如果不符合特殊条件就不行。 如果想表达其中两个条件组合,排斥第三个条件,那就是在连线上标注。 如果想表达其中一个条件单独满足,同时不考虑其他三个条件,你就选这个点。 |
|
|
五维互斥信息图也有,因为欧拉多面体包括正20面体,可以切分成五块完全相似的单元,涂色之后互斥关系一目了然。 |

|
|
但是,为什么没有呢: 这里要推销我的媒体教程《第七课,控制内容深度》: 这里剧透一小段付费内容作为广告: |
|
|
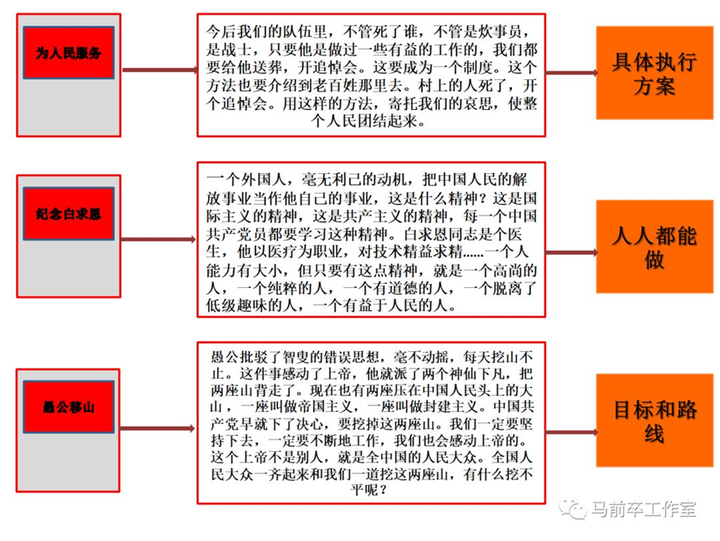
抛开政治和历史问题,仅从媒体视角看,《为人民服务》也是20世纪传播最广的一篇白话文演讲稿,现在还有几亿中国人能背出来。作为资深撰稿人,毛泽东一辈子有4万多篇文章和讲话记录,《为人民服务》的影响力排到最前面,我们必须承认这是一篇在传播技巧上接近完美的作品,是媒体人必须严肃分析的案例。 具体到信息深度方面,《为人民服务》包含两个“转折点”这不是偶然。我总结十几年的经验教训,也认为传播性价比最高的信息挖掘深度就是2。下面具体解释一下。 |
|
|
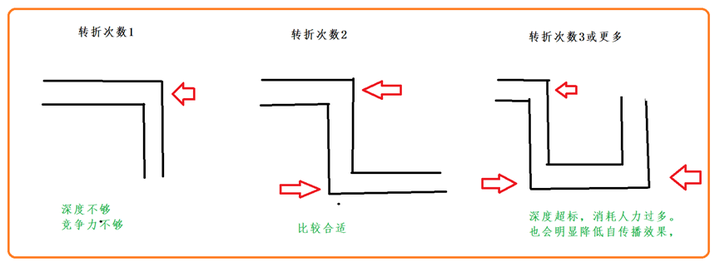
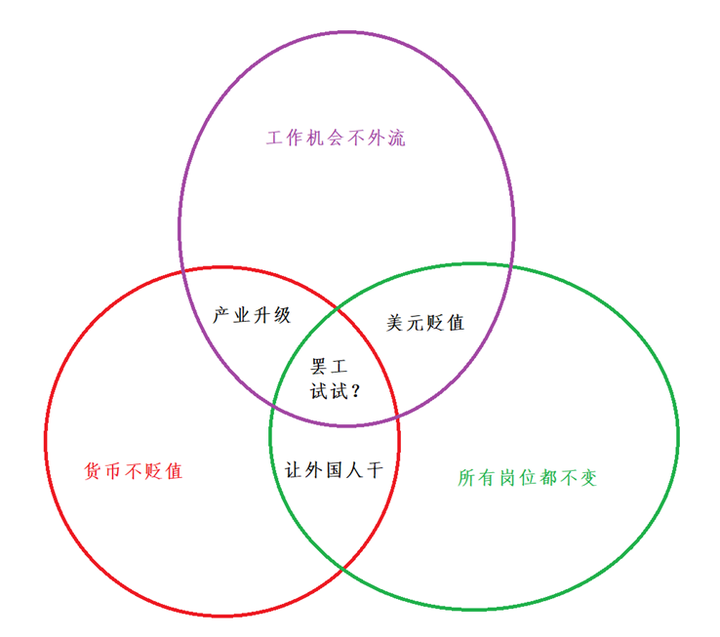
…… 如果媒体人坚持只做一层逻辑结构,多半就得买一送一,用情绪价值来补充观众的需求。所以我们经常看到单层逻辑的媒体产品拼命喊口号,加背景音乐,鼓吹种族仇恨和个人崇拜。但这些情绪价值也没什么门槛,竞争强度很大,如果你真的想和垃圾同行拉开差距,就得想办法把逻辑深度升级到第二层。 但随着“转折点”数量增加,媒体人投入的资源也必然以指数速度上升。用物理概念来说,每一次转折,内容都要在更高的维度中作选择。一次转折是从直线进入平面,二次转折就是从平面进入三维空间。空间导航、或者说建立逻辑线条的难度越来越大。 ……. 老观众可能知道,睡前消息节目经常有一些风格粗暴的配图,往往是我用系统自带的绘图板画的。其中最常见的一类图,是三圆交错图。比如说653期节目介绍的美国汽车工人罢工问题: 逻辑链条可以从任何一个诉求开始,每加一个圆,就会增加一个逻辑转折点。把两个转折点解释清楚,中间的结论三角区就很明显了。三个诉求不可能同时满足,所以罢工行为包含了侥幸心理。 |
|
|
…… 但是,就像上面三个圆圈的图不能加第四个,在对比历史和现实,分析合理性的时候,四个要素配三个转折点,明显复杂性超标了,影响观众快速理解,快速转发。所以我根据历史相似性,实际上把19世纪的普鲁士案例和日本案例合并了,简化到三个历史阶段: …… 我根据经验建议,凡是有定期更新压力的媒体,如果没有国家资金支持,就要学习毛主席的写作风格,尽量把研究深度控制在2个转折点,只在非常有利的条件下考虑3个转折点。年度选题级别的重大项目,才敢设想4层以上的转折。 |
|
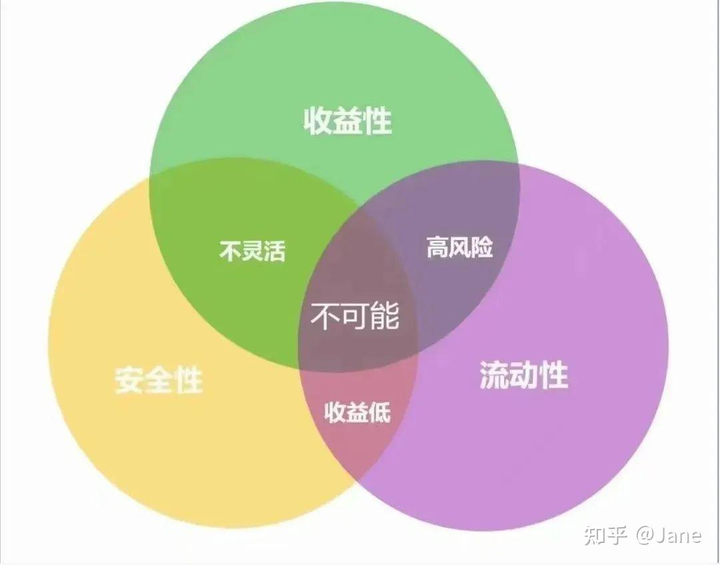
我很赞同这个问题下面的很多答主,以及 @睡前消息 马督工的观点,即这是个媒体传播社会学问题。马督工的回答在前面铺垫了一些数学,但很不巧是错的。于是我这篇回答偏个题,讲一些数学,也当作对他回答的补充。 我们可以定义一个“不可能 n 角”,它是一个包含 n 个元素的集合 V=\{v_1, v_2,\dots, v_n\} ,以及 V 的子集族 K(V) ,由于 V 的一个子集 都有“是”或“否”含有 v_i 两种取法,所以 V 一共包含 2^n 个不同的子集,即 K 有 2^n 个元素。 以“不可能 3 角”为例: |
|
|
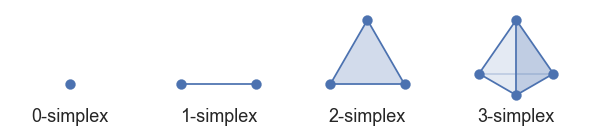
在这个例子中,我们记 \{v_1\} 为“收益性”, \{v_2\} 为“安全性”, \{v_3\} 为“流动性”,那么 \{v_1, v_2\} 是“不灵活”, \{v_1, v_3\} 是“高风险”, \{ v_2, v_3\} 是“收益低”, \{v_1, v_2, v_3\} 就是“不可能”,如果把空集 \varnothing 定义成“什么都不要求”,那么 K(V)=\{\{v_1\}, \{v_2\}, \{v_3\}, \{v_1,v_2\},\{v_1,v_3\},\{v_2,v_3\}, \{v_1, v_2, v_3\}, \varnothing\} 这个含 2^3=8 个元素的集合就能代表所有的情况。对于 “不可能 n 角”,只需做类似的推广即可。 当然,我们现在只是从“组合”的角度解决了这个问题,而科普,或者媒体,往往要搞一点可视化,来便于读者理解,因此我们需要引入几何,而非抽象的代数(组合)。这个时候就可以引入“单纯形”(simplex,简称单形)的概念。我们可以把 V=\{v_1, v_2,\dots, v_n\} 对应到 n 维欧氏空间 \mathbb R^n 中的 n 个“线性无关”的点,比如可以取 v_1=(0,0,\dots, 0) , v_2=(1, 0,\dots, 0) ,... , v_n=(0,0,\dots, 1) ,它们的“凸组合” \{x | x=\sum_{i=1}^n \lambda_i v_i, \sum_{i=1}^n\lambda_i=1, \lambda_i\geqslant 0\}\subseteq \mathbb R^n 就称作一个“ n-单形”。 这时候 m\leqslant n 个点的子集 \{v_{k_1},v_{k_2},\dots v_{k_m}\} 就表示由这 m 个点“凸组合”成的 m-单形,显然它是原先 n-单形的一个“广义的面”。 例如: |
|
|
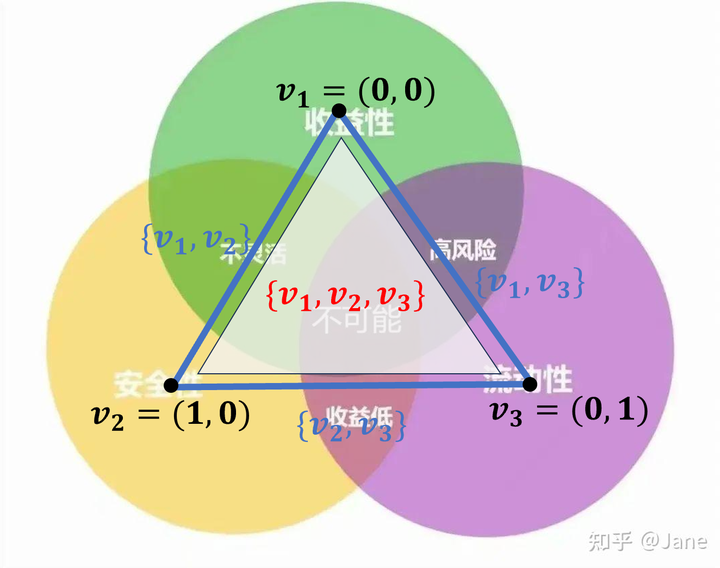
1-单形就是一条线段,2-单形是一个三角形,3-单形是一个四面体。 回到上面“不可能3角”的例子,我们可以用 2-单形实现一个可视化。请允许我直接把 2-单形盖在了原图上: |
|
|
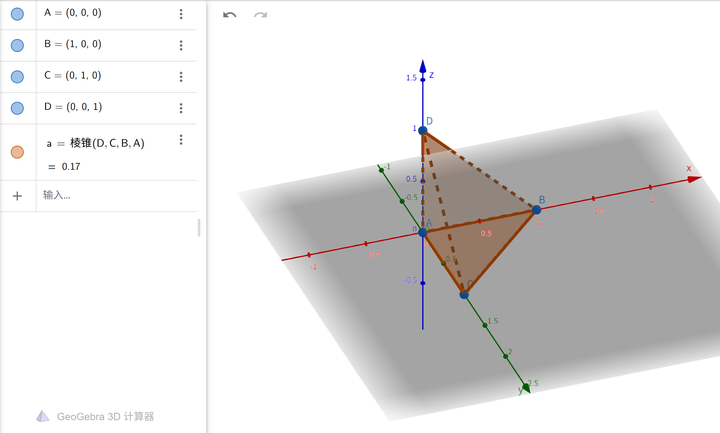
这样表示2单形的三角形就代表了“不可能”,它的三条边就代表了两个元素组合的情况。 那么“不可能4角”的情况如何呢?事实上我们可以在空间(3维),而非平面(2维)上实现它: |
|
|
这是一个“3-单形”,其中,3维的四面体可以表示一个状态,它的四个2维的三角形面可以表示4个状态,他的6个1维的棱可以表示6个状态,四个0维的顶点表示4个状态,加上“什么都不干”,一共是 2^4=16 种状态。 如果技术发达到人们可以轻松观察“立体影像”,我猜“不可能4角”会更方便可视化,应用也会更广泛些。 那么“不可能5角”是什么情况?很遗憾的是,它无法在三维空间里用“4-单形”实现可视化。从两个角度解释:“4-单形”是一个四维对象,如果要把它塞到3维空间里必然会“坍缩”一个维度。另一方面,线性代数的知识告诉我们,张成4-单形的5个线性无关的点,可以构成4个线性无关的向量,然而三维空间至多允许3个线性无关向量。 马督工犯的错误也在于此: |

|
|
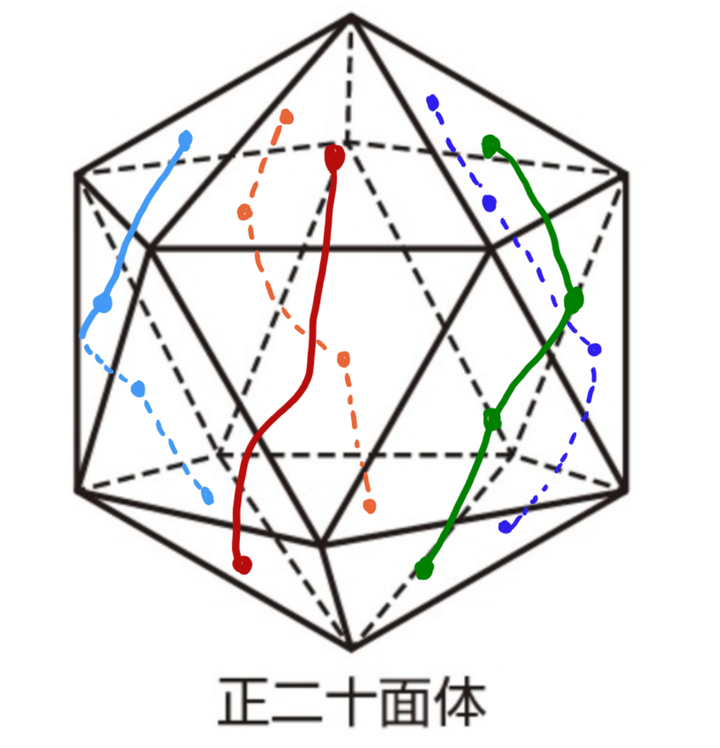
他想当然地把正二十面体的20个面分成5份,每份含4个面,用这5份的“相邻关系”来表示5个元素之间的全部关系。事实上,他给出的这种剖分方式,每份也只和两组相邻。 |
|
|
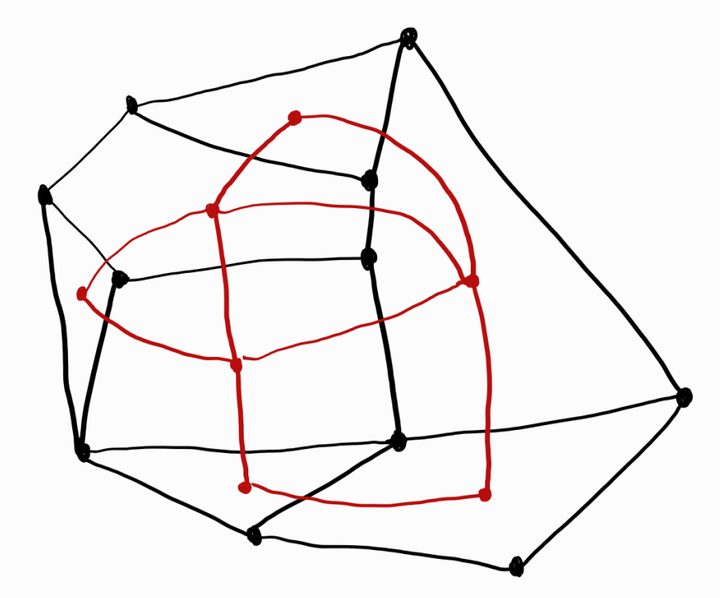
图示为按照马督工的想法分组,这里每组用不同的颜色衔接 这种剖分方式就好比给地球划分“时区”,每份就好像是用地球上的两条经线划分出来的,因此也只和两份相邻。 事实上,不管马督工怎么努力,也不可能找到正二十面体(甚至随便一个球面的三角形剖分)能满足“任意两份都相邻”的5份。 任取一种划分方式,只考虑每份的共同边界围成的区域,就相当于把地球分成了5份,每份在一段边界上相邻。这时候我们取这张“地图”的对偶图,即在每块区域的内部取一点,如果两片区域相邻,那么穿过它们的共同边界连一条线,连接这两个面上的点。 |
|
|
对偶图示意图 这里黑色的线围成一张地图,红色的线表示它的“对偶图”。 假若真的每两块区域都相邻,那么对偶图就实现为了“完全图” K_5 ,即一个含有5个顶点的图,且每两个顶点都由一条棱连接起来。然而,图论中的 Kuratowski 定理说: K_5 不是平面图。由于球面和平面“只差一个点”(你可以想象,把一个气球戳破一个洞,用剩下的球膜可以铺满平面), K_5 同样也不能是球面上的图,这就产生了一个矛盾。 |
|
|
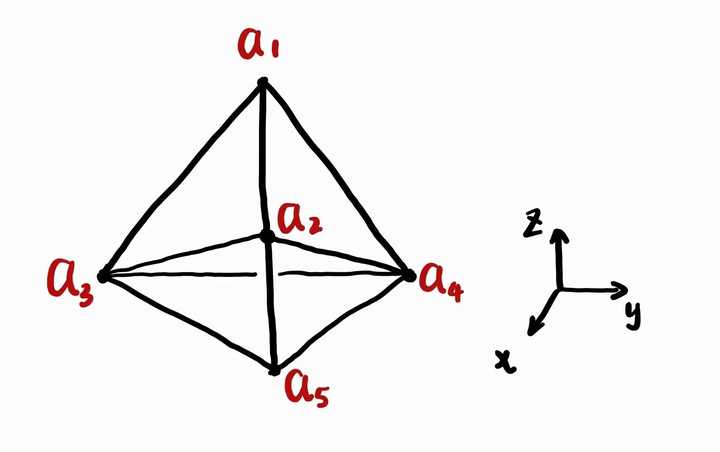
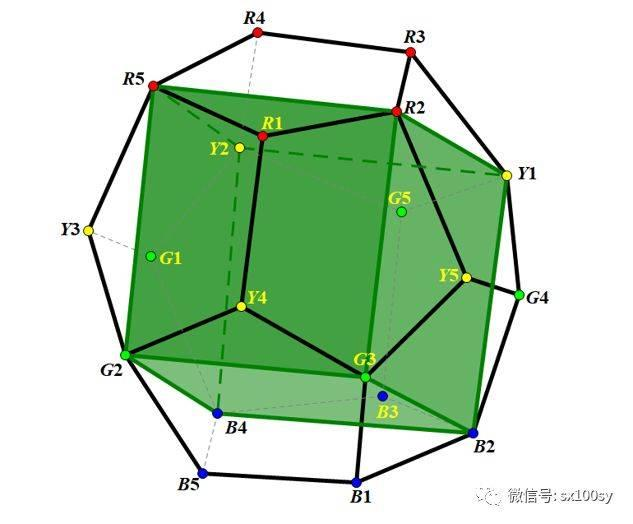
这张图表示:尽管 K_5 不能嵌入2维平面,但可以嵌入三维空间,但也只能表示全部“两个元素”的关系,如果想表示“三个元素”的关系,给三个顶点之间填上三角形即可。但如果想表示四个元素的关系,那么不同的四面体之间就会产生相交(比如 a_1a_2a_3a_4 与 a_1a_3a_4a_5 相交)。因此表示“不可能5角”的理想几何模型生活在4维空间,但可惜人类缺乏四维空间的直观。 不过我想马督工下意识想用“正二十面体”来解释5个元素的关系也不完全是“无中生有”,正二十面体还真跟“5”有点关系。事实上,“正二十面体”的“旋转对称群”同构于 A_5 ,即5个元素的偶置换。 于是我们再次偏题更远一点: 为了绘图方便,我们考虑与正二十面体对偶的正十二面体: 正十二面体有5个顶点重合的内接正立方体(五边形面的任意一条对角线都决定唯一一个这样的正立方体): |
|
|
不计每个立方体的顶点顺序,只考虑它们彼此之间在旋转作用下的置换,可以检查到:如果正二十面体在三维欧式空间的一个旋转下不变(旋转后与原来重合),那么这个旋转导致了5个内接正立方体的偶置换。且恰好旋转的方式共有60种,与5个元素的偶置换的个数相同,即正十二面体(或正二十面体)的对称群同构于 A_5 。 然而,“偶置换群”与“5个元素的组合关系”,在我看来毫不相关。 |
|
米勒定律又称“7±2 法则”。 米勒定律表示人类头脑最好的状态能记忆7(±2)个信息块(即5~9个)。 也就是说超过9个信息块之后,大多数人就记不住了。 三个元素可以产生8种组合,在米勒定律的限度内,刚好能被人记住。 |
|
|
| [收藏本文] 【下载本文】 |
| 人物音乐 最新文章 |
| 单从唱功来说王菲跟萨顶顶谁更厉害? |
| 有哪些歌词听错反而更有意境? |
| 如何评价 2026 年春晚海来阿木演唱、刘浩存 |
| 国产电吉他和进口电吉他差距究竟在哪里? |
| 高骈此人如何评价? |
| 洛天依新歌被曝抄袭薛之谦,发行方已开除相 |
| 如何评价小提琴家陈锐(Ray Chen)? |
| 你认为aespa的实力排名? |
| 为什么孙楠、韩红版的《美丽的神话》被成龙 |
| 张敬轩和关智斌是真的吗? |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
|
古典名著
名著精选
外国名著
儿童童话
武侠小说
名人传记
学习励志
诗词散文
经典故事
其它杂谈
小说文学 恐怖推理 感情生活 瓶邪 原创小说 小说 故事 鬼故事 微小说 文学 耽美 师生 内向 成功 潇湘溪苑 旧巷笙歌 花千骨 剑来 万相之王 深空彼岸 浅浅寂寞 yy小说吧 穿越小说 校园小说 武侠小说 言情小说 玄幻小说 经典语录 三国演义 西游记 红楼梦 水浒传 古诗 易经 后宫 鼠猫 美文 坏蛋 对联 读后感 文字吧 武动乾坤 遮天 凡人修仙传 吞噬星空 盗墓笔记 斗破苍穹 绝世唐门 龙王传说 诛仙 庶女有毒 哈利波特 雪中悍刀行 知否知否应是绿肥红瘦 极品家丁 龙族 玄界之门 莽荒纪 全职高手 心理罪 校花的贴身高手 美人为馅 三体 我欲封天 少年王 旧巷笙歌 花千骨 剑来 万相之王 深空彼岸 天阿降临 重生唐三 最强狂兵 邻家天使大人把我变成废人这事 顶级弃少 大奉打更人 剑道第一仙 一剑独尊 剑仙在此 渡劫之王 第九特区 不败战神 星门 圣墟 |
|
|
| 网站联系: qq:121756557 email:121756557@qq.com |