[明星艺术] 蛇年将至，如何用你的兴趣/专业技能画一条蛇？

阅读网购物网址万年历小说 | 三丰软件天天财富小游戏

TxT小说阅读器
↓小说语音阅读,小说下载↓

一键清除系统垃圾
↓轻轻一点,清除系统垃圾↓

图片批量下载器
↓批量下载图片,美女图库↓

图片自动播放器
↓图片自动播放,产品展示↓

佛经: 故事佛经佛经精华心经金刚经楞伽经南怀瑾星云法师弘一大师名人学佛佛教知识标签

名著: 古典现代外国儿童武侠传记励志诗词故事杂谈道德经讲解词句大全词句标签哲理句子

网络: 舞文弄墨恐怖推理感情生活潇湘溪苑瓶邪原创小说故事鬼故事微小说耽美师生内向易经后宫鼠猫美文

教育信息历史人文明星艺术人物音乐影视娱乐游戏动漫 | 穿越校园武侠言情玄幻经典语录三国演义西游记红楼梦水浒传

阅读网 -> 明星艺术 -> 蛇年将至，如何用你的兴趣/专业技能画一条蛇？ -> 正文阅读

[明星艺术]蛇年将至，如何用你的兴趣/专业技能画一条蛇？

[收藏本文] 【下载本文】

代码画蛇、数学答主公式画蛇、骑行路线、跑步路线画蛇、剪纸、游戏创建蛇岛、我的世界搭建一个蛇…你会怎么创作呢？蛇年有奖活动： https://www.…

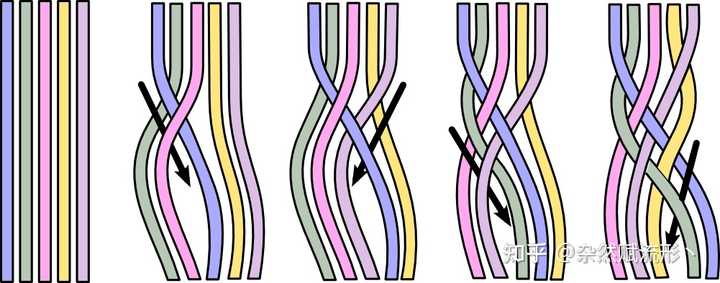
我来提一下数学中辫群（braid group）的概念。
辫群是数学中低维拓扑里最具有吸引力的理论之一，它不仅有自然的几何直观表现，还与数学中的扭结、链环等结构有密切联系。除此之外，它还在量子物理、拓扑量子计算、凝聚态物理等多个领域有广泛应用。
一个著名的例子便是任意子，和传统的玻色子、费米子不同，任意子之间的交换会使得波函数出现非平凡的相位因子，它们的统计行为需要用辫群的表示来描述。
简单来说，辫群 Bn" role="presentation">BnB_n 描述了 n" role="presentation">nn 个元素在空间中的相互交换，可以将其想象为多个绳子相互交织、扭转的过程，一个例子如下图所示：

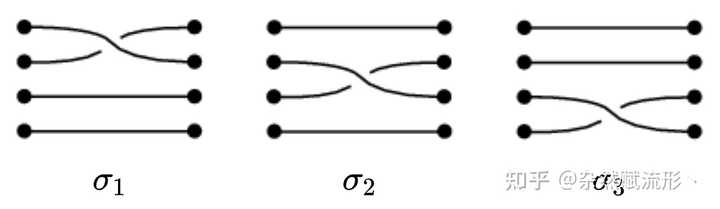
5 根绳子的缠绕，每一种编织方式都代表了辫群 B_5 的一个元素
辫群 Bn" role="presentation">BnB_n 有 n−1" role="presentation">n?1n-1 个生成元 σ1,σ2,⋯,σn−1" role="presentation">σ1,σ2,?,σn?1\sigma_1,\sigma_2,\cdots,\sigma_{n-1} ，其中 σi" role="presentation">σi\sigma_i 代表的是第 i" role="presentation">ii 和第 i+1" role="presentation">i+1i+1 根绳子之间的交换，这个交换操作通常被称为「交叉」或「扭结」，这些交错的结构正是我们所说的「蛇形」图形的基础。
辫群 Bn" role="presentation">BnB_n 可以表示成 Bn=⟨σ1,…,σn−1∣σiσi+1σi=σi+1σiσi+1, σiσj=σjσi⟩" role="presentation">Bn=?σ1,…,σn?1∣σiσi+1σi=σi+1σiσi+1, σiσj=σjσi?B_n = \left\langle\sigma_1,\dots,\sigma_{n-1} \mid \sigma_{i}\sigma_{i+1}\sigma_{i} = \sigma_{i+1}\sigma_{i}\sigma_{i+1}, \ \sigma_{i}\sigma_j = \sigma_j \sigma_i \right\rangle ，其中右边第一个关系式中 1≤i≤n−2" role="presentation">1≤i≤n?21\leq i \leq n-2 ，第二个关系式中 |i−j|≥2" role="presentation">|i?j|≥2|i-j|\geq 2 。
例如我们考虑 4 根绳子的缠绕，所组成的辫群 B4" role="presentation">B4B_4 有 3 个生成元，如下图所示：

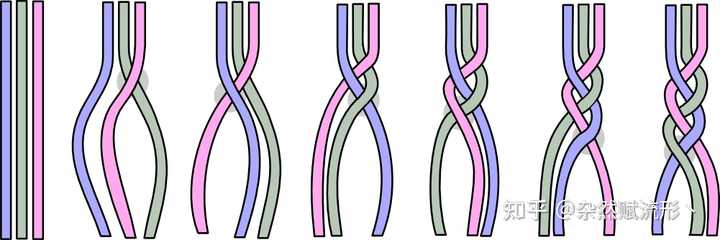
辫群 B_4 的 3 个生成元，其他编织结构均可以通过这三个元素的复合构成
值得一提的是，一维曲线只能在三维空间中打结，所以任意子是一个二维空间（即 2+1 维时空）中的物理。对于一个三维空间（即 3+1 维时空），一个粒子的世界线（对应前述的 1 维曲线）显然无法在 3+1 维时空中打结，因此描述三维空间粒子的统计行为需要用到的是置换群 Sn" role="presentation">SnS_n 而非辫群 Bn" role="presentation">BnB_n ，这也是为什么三维空间中只有玻色子和费米子的一个原因。
虽然辫群 Bn" role="presentation">BnB_n 和置换群 Sn" role="presentation">SnS_n 不同，但存在唯一一个群同态 π:Bn→Sn" role="presentation">π:Bn→Sn\pi:B_n\to S_n ，满足 si=π(σi)" role="presentation">si=π(σi)s_i = \pi(\sigma_i) , ∀i=1,2,…,n−1" role="presentation">?i=1,2,…,n?1\forall i=1,2,\dots,n-1 。同态 π:Bn→Sn" role="presentation">π:Bn→Sn\pi:B_n\to S_n 的核即为我们通常所说的单纯辫群 Pn=Ker(π:Bn→Sn)" role="presentation">Pn=Ker(π:Bn→Sn)P_n = \mathrm{Ker}(\pi:B_n\to S_n) 。
至此，我们简单介绍了辫群 Bn" role="presentation">BnB_n 的概念，通过辫群的生成元，我们可以构造出更复杂的交织结构，类似于蛇体在空间中扭曲、盘绕的形态。每一个交换操作对应着空间中「绳子」间的交织，而这些交织正是蛇形轨迹的几何表现。

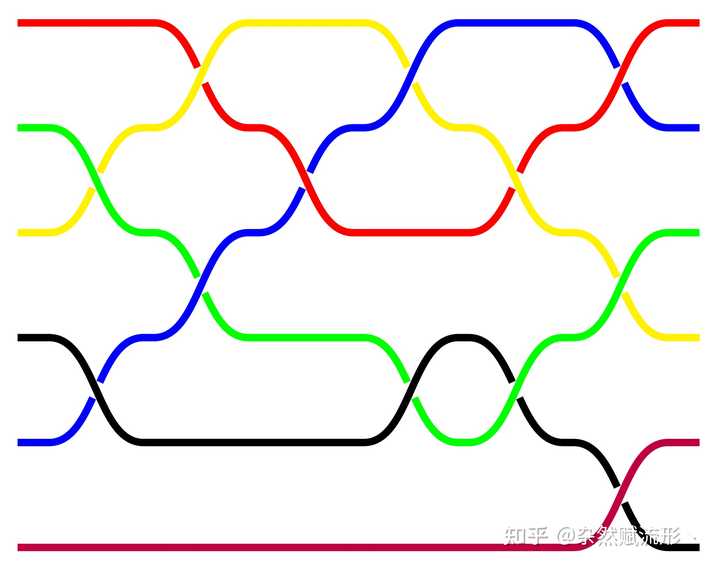
三根绳子编织过程示例
但如何画出复杂的编织结构呢？
别急，我们可以交给 LATEX" role="presentation">LATEX\mathrm{\LaTeX} ，它有一个非常好用的宏包 braids，可以方便地画出各种编织，如下图所示，给出了 6 根绳子彼此编织的复杂结构，

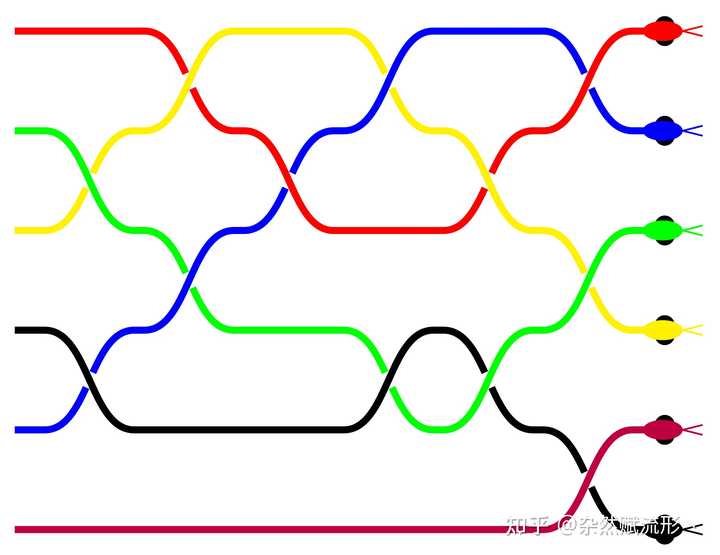
6 根绳子彼此编织的复杂结构
接下来，我们只需要加一点点细节，画上蛇的头部即可，最终效果如下图所示：

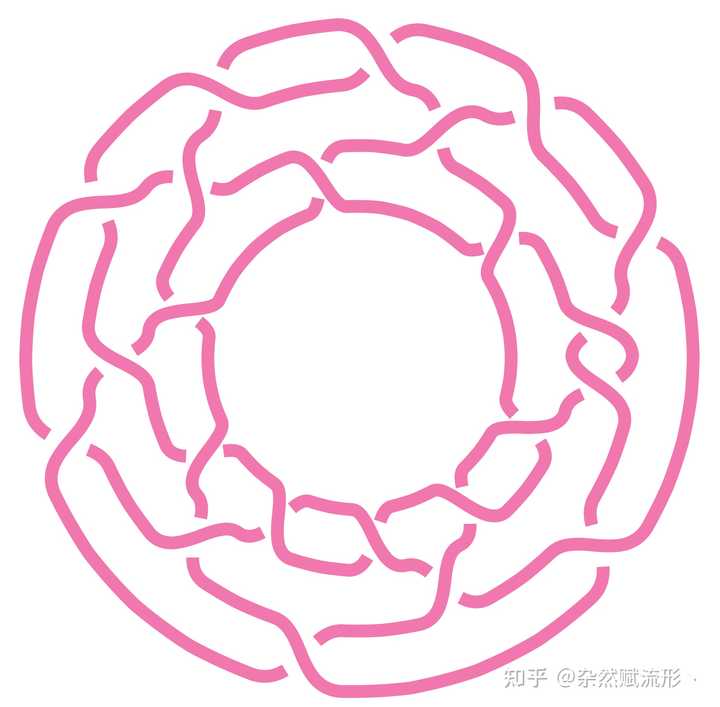
使用 LaTeX 的 braids 宏包绘制出的六条蛇
实现代码：

\documentclass[border=10pt]{standalone}
\usepackage{tikz}
\usetikzlibrary{braids}
\newcommand{\snake}[2]{
    \fill (#1-0.05, 0.02) circle (0.1);
    \fill (#1+0.05, 0.02) circle (0.1);
    \fill[#2] (#1,0) ellipse (0.1 and 0.2);
    \draw[#2, line width=0.5pt] (#1, 0.2) -- (#1+0.05, 0.4);
    \draw[#2, line width=0.5pt] (#1, 0.2) -- (#1-0.05, 0.4);
}

\begin{document}
\begin{tikzpicture}[rotate=-90]
  % 辫图
  \pic[
  rotate=-90,
  line width=2pt,
  braid/strand 1/.style={red},
  braid/strand 2/.style={blue},
  braid/strand 3/.style={green},
  braid/strand 4/.style={yellow},
  braid/strand 5/.style={purple},
  braid/add floor={2,4,3,2},
  name=coordinates,
  ] at (0,0) {braid={| s_1-s_3-s_5 | s_2^{-1}-s_4| s_1-s_4 s_2^{-1}
  s_1-s_3 s_2^{-1}-s_4^{-1}}};

  % 蛇的头部
  \snake{0}{red};
  \snake{1}{blue};
  \snake{2}{green};
  \snake{3}{yellow};
  \snake{4}{purple};
  \snake{5}{black};
\end{tikzpicture}
\end{document}

当然你也可以继续整一些花活，例如文档里展示了绘制花朵的一个例子：

使用 LaTeX 的 braids 宏包绘制出的花朵
实现代码：

\documentclass[border=10pt]{standalone}
\usepackage{tikz}
\usetikzlibrary{braids}
\usepgfmodule{nonlineartransformations}
\makeatletter
\def\polartransformation{%
% \pgf@x will contain the radius
% \pgf@y will contain the distance
\pgfmathsincos@{\pgf@sys@tonumber\pgf@x}%
% pgfmathresultx is now the cosine of radius and
% pgfmathresulty is the sine of radius
\pgf@x=\pgfmathresultx\pgf@y%
\pgf@y=\pgfmathresulty\pgf@y%
}
\makeatother

\begin{document}
\begin{tikzpicture}[scale=.5]
  \begin{scope}
  \pgftransformnonlinear{\polartransformation}% see above
  \pic[
  rotate=90,
  braid/.cd,
  every strand/.style={line width=6pt,magenta!67},
  border height=0cm,
  crossing height=15.7pt,
  gap=.2,
  nudge factor=0.01,
  ] at (0,5) {braid=%
  s_2^{-1} s_3 s_1 s_3 s_2^{-1} s_3 s_1 s_3
  s_2^{-1} s_3 s_1 s_2^{-1} s_3 s_1 s_2^{-1}
  s_1 s_3 s_1 s_2^{-1} s_1 s_3 s_1 s_2^{-1}
  };
  \end{scope}
\end{tikzpicture}
\end{document}

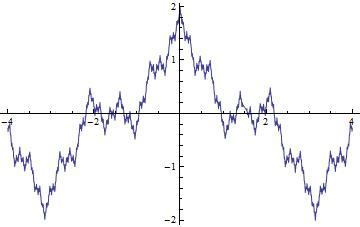
画一条连续但是处处不可导的蛇——威尔斯特拉斯函数
f(x)=∑k=0∞akcos⁡(bkπx)," role="presentation">f(x)=∑k=0∞akcos?(bkπx),\begin{align*}f(x)=\sum_{k=0}^\infty a^k \cos(b^k \pi x),\end{align*}
其中 0<a<1" role="presentation">0<a<1b 是正奇数，且满足1+\frac{3\pi}{2},\end{align*}">ab>1+3π2," role="presentation">ab>1+3π2,\begin{align*}ab>1+\frac{3\pi}{2},\end{align*} 例如 a=5/6, b=7" role="presentation">a=5/6, b=7a=5/6,\ b = 7 或者 a=1/2, b=13." role="presentation">a=1/2, b=13.a=1/2,\ b = 13.

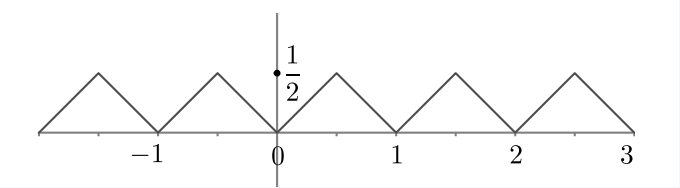
关于Weierstrass函数的不可导证明非常复杂，具体证明可以参见这篇论文。
https://people.math.aau.dk/~jjohnsen/Articles/WEBfiler/nowhere.pdf?people.math.aau.dk/~jjohnsen/Articles/WEBfiler/nowhere.pdf
我们再构造一个例子叫做Blancmange Curve，并给出它是一个连续却处处不可导的曲线的证明，给大家对于这类性质函数的一个直观的理解。
考虑函数 f1(x)=|x−round(x)|" role="presentation">f1(x)=|x?round(x)|f_1(x)=|x-\textrm{round}(x)| ，即 x" role="presentation">xx 和距离它最近的整数之间的距离。容易看出，这个函数的周期为 1" role="presentation">11 ，在所有 x=k/2" role="presentation">x=k/2x=k/2 （ k" role="presentation">kk 是整数）处不可导。

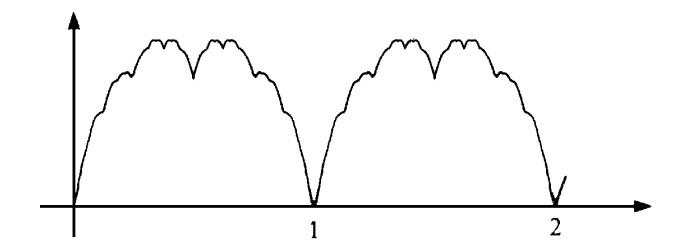
接下来定义 f2(x)=f1(2x)/2" role="presentation">f2(x)=f1(2x)/2f_2(x)=f_1(2x)/2，这个函数周期为 1/2" role="presentation">1/21/2 ，在所有 x=k/4" role="presentation">x=k/4x=k/4 （ k" role="presentation">kk 是整数）处不可导。
以此类推，定义 fn(x)=fn−1(2n−1x)/2n−1" role="presentation">fn(x)=fn?1(2n?1x)/2n?1f_n(x)=f_{n-1}(2^{n-1} x)/2^{n-1}（ n" role="presentation">nn 是正整数），这个函数周期为 1/2n−1" role="presentation">1/2n?11/2^{n-1} ，且在所有 x=k/2n" role="presentation">x=k/2nx=k/2^n （ k" role="presentation">kk 是整数）处不可导。
可以看到随着 n" role="presentation">nn 的增加，函数的周期越来越小，不可导的点在任意有限长度区间（例如 [0,1]" role="presentation">[0,1][0,1] 上）变得越来越多。
最后定义 F(x)=∑n=1∞fn(x)" role="presentation">F(x)=∑n=1∞fn(x)\begin{align*}F(x)=\sum_{n=1}^\infty f_n(x)\end{align*} ，图像如下：

下面证明 F" role="presentation">FF 的连续性和处处不可导性。
性质1（连续性）：
首先 F(x)" role="presentation">F(x)F(x) 取值在 [0,1]" role="presentation">[0,1][0,1] 之间，因为 0≤F(x)≤∑n=1∞12n=1." role="presentation">0≤F(x)≤∑n=1∞12n=1.\begin{align*}0\le F(x)\le \sum_{n=1}^\infty \dfrac{1}{2^{n}}=1.\end{align*}
对于任意一点 x0" role="presentation">x0x_0 和 0,">ϵ>0," role="presentation">?>0,\epsilon>0, 注意到 F(x)=∑n=1mfn(x)+12mF(2mx)" role="presentation">F(x)=∑n=1mfn(x)+12mF(2mx)\begin{align*}F(x)=\sum_{n=1}^{m}f_n(x)+\dfrac{1}{2^m}F(2^m x)\end{align*}(自相似性）。我们选择足够大的 m" role="presentation">mm 使得 1/2m<ϵ/2" role="presentation">1/2m<?/2f_n(x) 是连续的，选择 0">δ>0" role="presentation">δ>0\delta>0 使得 |fn(x)−fn(x0)|<ϵ/2m" role="presentation">|fn(x)?fn(x0)|<?/2mn=0,1,\ldots,m-1 都成立，于是
|F(x)−F(x0)|≤m⋅ϵ2m+ϵ2=ϵ." role="presentation">|F(x)?F(x0)|≤m??2m+?2=?.|F(x)-F(x_0)|\le m\cdot \dfrac{\epsilon}{2m}+\dfrac{\epsilon}{2}=\epsilon.
因此 F" role="presentation">FF 连续。
性质2（处处不可导）：
考虑任意一点 x0" role="presentation">x0x_0 ，对于任何一个 h=2−m" role="presentation">h=2?mh=2^{-m} (m" role="presentation">mm 为正整数）可以找到整数 s" role="presentation">ss 使得 um=s2m" role="presentation">um=s2mu_m=\dfrac{s}{2^m} 和 vm=s+12m" role="presentation">vm=s+12mv_m=\dfrac{s+1}{2^m} 满足um≤x0<vm." role="presentation">um≤x0<vm.f_k(u_m)=f_k(v_m)=0 对于 m">k>m" role="presentation">k>mk>m , 我们有
F(vm)−F(um)vm−um=∑n=1mfn(vm)−fn(um)vm−um." role="presentation">F(vm)?F(um)vm?um=∑n=1mfn(vm)?fn(um)vm?um.\begin{align*}\dfrac{F(v_m)-F(u_m)}{v_m-u_m}=\sum_{n=1}^m \dfrac{f_n(v_m)-f_n(u_m)}{v_m-u_m}.\end{align*}
而由于 f_n 在 [u_m,v_m] 上是线性的， \dfrac{f_n(v_m)-f_n(u_m)}{v_m-u_m} 一定等于 1 或者 -1，因此
\begin{align*}\dfrac{F(v_m)-F(u_m)}{v_m-u_m}=\sum_{n=1}^m \pm 1\equiv m(\text{mod }2).\end{align*}
随着 h\to 0, \dfrac{F(v_m)-F(u_m)}{v_m-u_m}极限不存在（奇偶性在不断变化），即在 x_0 处不可导。

Python意为蟒蛇，Python 的 Logo 也是两条缠绕在一起的蟒蛇，今年也算是Python的本命年了。
先画个简单地：

import turtle

def setup_window(width=650, height=350, start_x=200, start_y=200):
    """设置窗口大小和初始位置"""
    turtle.setup(width, height, start_x, start_y)

def move_to_start_position():
    """移动蛇到起始位置"""
    turtle.penup()
    turtle.goto(-250, 0)  # 移动到左边开始画
    turtle.pendown()

def configure_turtle(pen_size=25, pen_color="red", initial_heading=-40):
    """配置蛇属性"""
    turtle.pensize(pen_size)
    turtle.pencolor(pen_color)
    turtle.seth(initial_heading)

def draw_pattern():
    """绘制图案"""
    for _ in range(4):
        turtle.circle(40, 80)
        turtle.circle(-40, 80)
    turtle.circle(40, 40)  # 80/2 = 40
    turtle.fd(40)
    turtle.circle(16, 180)
    turtle.fd(40 * 2 / 3)

def main():
    try:
        setup_window()
        move_to_start_position()
        configure_turtle()
        draw_pattern()
        turtle.done()
    except Exception as e:
        print(f"发生错误: {e}")
        turtle.bye()  # 关闭窗口

if __name__ == "__main__":
    main()

用python代码画下这个双头蟒的LOGO：

自己尝试写了下，效果很差，不献丑了，在此引用网友代码：https://blog.csdn.net/weixin_55865873/article/details/124359141" data-tooltip-richtext="1" data-tooltip-preset="white" data-tooltip-classname="ztext-reference-tooltip">[1]

import turtle as t

# 初始化颜色模式和画笔速度、粗细
t.colormode(255)
t.speed(10)
t.pensize(3)

# 将画笔移动到绘制起始位置
t.pu()
t.goto(-200,105)

# 开始绘制蓝色区域
t.pencolor(54,110,157)
t.fillcolor(54,110,157)
t.begin_fill()
t.goto(-225,-115)
t.pd()
t.seth(90)
t.fd(55)
t.circle(-50,90)
t.fd(190)
t.circle(50,90)
t.fd(100)
t.circle(85,90)
t.fd(100)
t.circle(85,90)
t.fd(30)
t.left(90)
t.fd(150)
t.seth(270)
t.fd(20)
t.right(90)
t.fd(220)
t.circle(50,90)
t.fd(105)
t.circle(50,90)
t.fd(50)
t.left(90)
t.end_fill()

# 在蓝色区域内绘制白色圆形
t.fillcolor(255,255,255)
t.pu()
t.goto(-125,155)
t.pd()
t.pencolor(255,255,255)
t.begin_fill()
t.circle(20,360)
t.end_fill()

# 开始绘制黄色区域
t.pu()
t.goto(85,80)
t.pd()
t.pencolor(255,212,69)
t.fillcolor(255,212,69)
t.begin_fill()
t.seth(270)
t.fd(55)
t.circle(-50,90)
t.fd(190)
t.circle(50,90)
t.fd(100)
t.circle(85,90)
t.fd(100)
t.circle(85,90)
t.fd(30)
t.left(90)
t.fd(150)
t.right(90)
t.fd(20)
t.right(90)
t.fd(220)
t.circle(50,90)
t.fd(105)
t.circle(50,90)
t.fd(50)
t.end_fill()

# 在黄色区域内绘制白色圆形
t.fillcolor(255,255,255)
t.pu()
t.goto(-10,-180)
t.pd()
t.pencolor(255,255,255)
t.begin_fill()
t.circle(20,360)
t.end_fill()

# 绘制完成，显示图形
t.done()

参考^用python的turtle库画一个python的logo https://blog.csdn.net/weixin_55865873/article/details/124359141

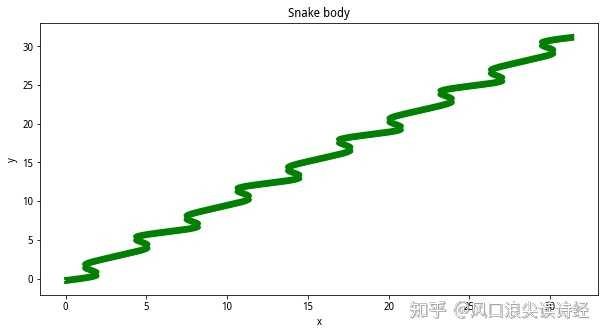
数学专业，用数学公式画一条蛇吧。
蛇的形状是弯弯曲曲的，用几个正弦函数搞出点不规则弯曲感，生成一个类似蛇形状的曲线。
x=y+sin(2y)+0.3sin(3y)
把公式用python画出来：

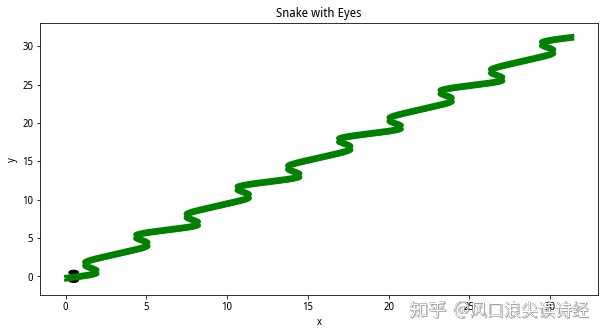
得加眼睛，画蛇点睛嘛，要不这蛇看着不灵动。这个简单，两个圆形。

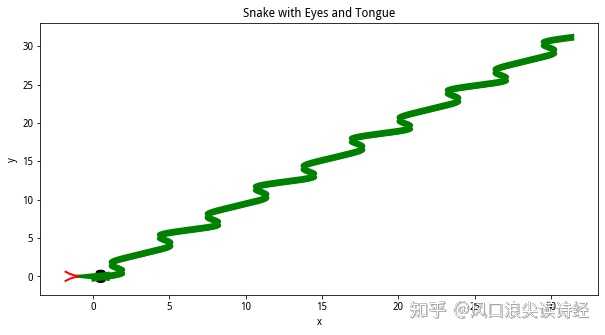
再加个三角形头部，画个舌头，妥了。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
plt.figure(figsize=(10,5))
# 参数范围
t = np.linspace(0, 10 * np.pi, 1000)  # 从 0 到 10π，生成1000个点

# 蛇的身体（两条曲线表示宽度）
body_width = 0.5  # 蛇的宽度
x_body = t + np.sin(2 * t) + 0.3 * np.sin(3 * t)
y_body = t

# 生成两条平行曲线
x_body_outer = x_body
y_body_outer = y_body
x_body_inner = x_body
y_body_inner = y_body - body_width

# 蛇的头部（假设头部在 t=0 附近）
head_x = x_body[0]
head_y = y_body[0]
triangle_x = [head_x - 1, head_x, head_x + 1]
triangle_y1 = [head_y, head_y + 0.2, head_y + 0.4]
triangle_y2 = [head_y, head_y - 0.2, head_y - 0.4]
plt.plot(triangle_x, triangle_y1, color='green', linewidth=3)
plt.plot(triangle_x, triangle_y2, color='green', linewidth=3)

# 蛇的眼睛（两个小圆）
eye1 = Circle((head_x + 0.5, head_y + 0.5), radius=0.3, color='black')
eye2 = Circle((head_x + 0.5, head_y - 0.5), radius=0.3, color='black')

# 蛇的舌头（两条线段）
tongue_x = [head_x - 1, head_x - 1.5, head_x - 1.8]
tongue_y1 = [head_y, head_y + 0.3, head_y + 0.6]
tongue_y2 = [head_y, head_y - 0.3, head_y - 0.6]

# 绘制蛇的身体（两条曲线）
plt.plot(x_body_outer, y_body_outer, color='green', linewidth=3)
plt.plot(x_body_inner, y_body_inner, color='green', linewidth=3)

# 填充身体内部
plt.fill_between(x_body, y_body_outer, y_body_inner, color='green', alpha=1)

# 添加蛇的眼睛
ax = plt.gca()
ax.add_patch(eye1)
ax.add_patch(eye2)

# 添加蛇的舌头
plt.plot(tongue_x, tongue_y1, color='red', linewidth=2)
plt.plot(tongue_x, tongue_y2, color='red', linewidth=2)

# 设置图形

plt.title("Snake with Eyes and Tongue")
plt.xlabel("x")
plt.ylabel("y")
#plt.axis('equal')  # 保持比例
plt.show()

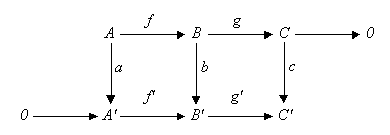
Lemma(Snake Lemma/蛇引理).http://www.shuxueji.com/w/2329" data-tooltip-richtext="1" data-tooltip-preset="white" data-tooltip-classname="ztext-reference-tooltip">[1]考虑一Abel范畴 \mathcal{A} 中的交换图:

Snake Lemma
使得每一横列均为正合序列. 此时存在一个联系 a,b,c 的核与上核的正合序列： \ker a\to\ker b\to \ker c\stackrel{d}{\longrightarrow}{\rm coker}\ a\to{\rm coker}\ b\to{\rm coker}\ c\\ 此外, 若 f 是单射, 则 \ker a\to\ker b 亦然; 若 g' 是满射, 则 {\rm coker}\ b\to{\rm coker}\ c 亦然.
参考^数学百科-同调代数-蛇引理 http://www.shuxueji.com/w/2329

[收藏本文] 【下载本文】

明星艺术最新文章

如何评价刘谦在 2025 年春晚表演的魔术《画

如何评价 2025 年春晚张艺谋导演的机器人舞

加:2025-01-27 22:25:48 更:2025-02-04 22:32:07

古典名著名著精选外国名著儿童童话武侠小说名人传记学习励志诗词散文经典故事其它杂谈
小说文学恐怖推理感情生活瓶邪原创小说小说故事鬼故事微小说文学耽美师生内向成功潇湘溪苑
旧巷笙歌花千骨剑来万相之王深空彼岸浅浅寂寞 yy小说吧穿越小说校园小说武侠小说言情小说玄幻小说经典语录三国演义西游记红楼梦水浒传古诗易经后宫鼠猫美文坏蛋对联读后感文字吧武动乾坤遮天凡人修仙传吞噬星空盗墓笔记斗破苍穹绝世唐门龙王传说诛仙庶女有毒哈利波特雪中悍刀行知否知否应是绿肥红瘦极品家丁龙族玄界之门莽荒纪全职高手心理罪校花的贴身高手美人为馅三体我欲封天少年王
旧巷笙歌花千骨剑来万相之王深空彼岸天阿降临重生唐三最强狂兵邻家天使大人把我变成废人这事顶级弃少大奉打更人剑道第一仙一剑独尊剑仙在此渡劫之王第九特区不败战神星门圣墟

网站联系: qq:121756557 email:121756557@qq.com