| |
|
| 阅读网 -> 明星艺术 -> 用 LaTeX 能画出哪些酷炫的图? -> 正文阅读 |
|
|
[明星艺术]用 LaTeX 能画出哪些酷炫的图? |
| [收藏本文] 【下载本文】 |
|
提问者在提问前已知晓存在更高效或更专业的绘图工具. 在不介意炫技的前提下,例如要为 ctexbook 制作扉页上的图案,那么你会想用 LaTeX 本身… |
|
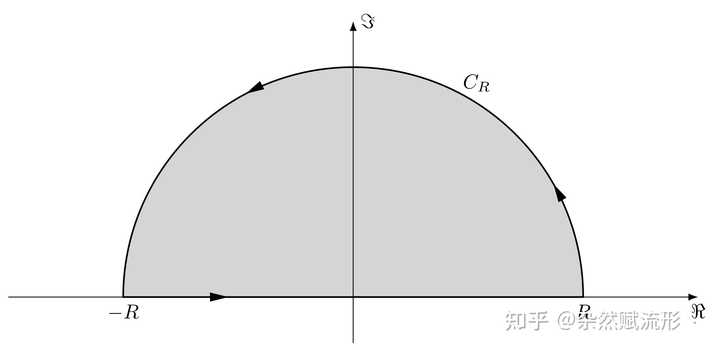
因为经常有人问我回答里的积分围道是怎么画出来的,所以我这里贴几个比较典型的 TikZ 代码示例供参考。 内容节选自: 杂然赋流形丶:【TikZ实例】复分析中的典型围道杂然赋流形丶:【TikZ实例】留数定理:你想要的积分围道都在这儿1. 半圆形围道: |
|
|
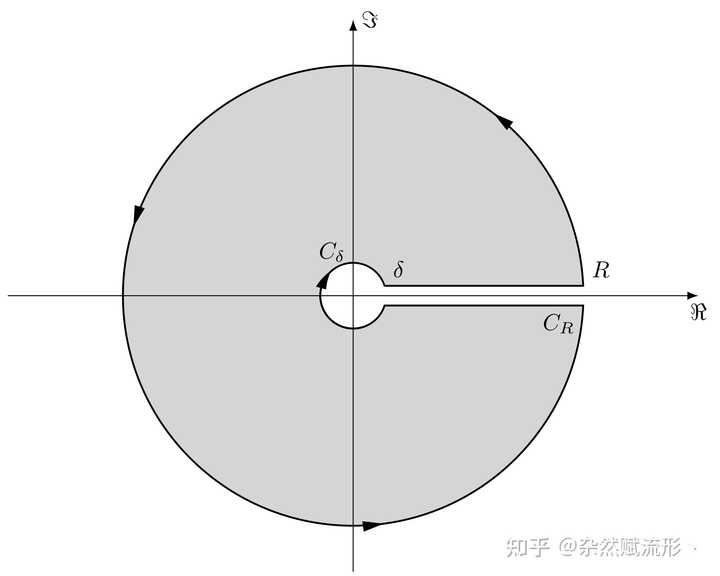
半圆形围道 2. 锁孔围道(keyhole 围道) |
|
|
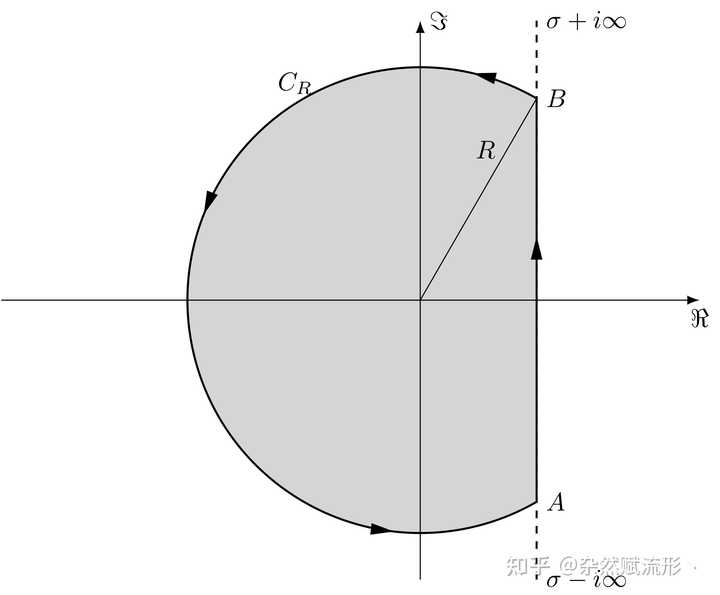
锁孔围道 3. Bromwich 围道 |
|
|
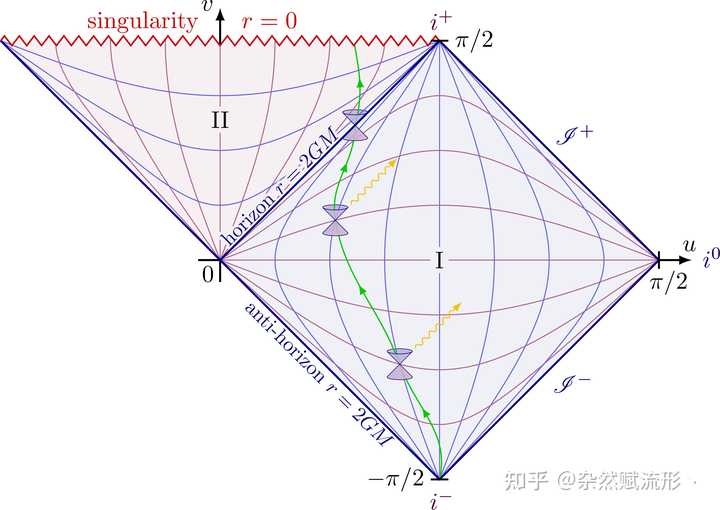
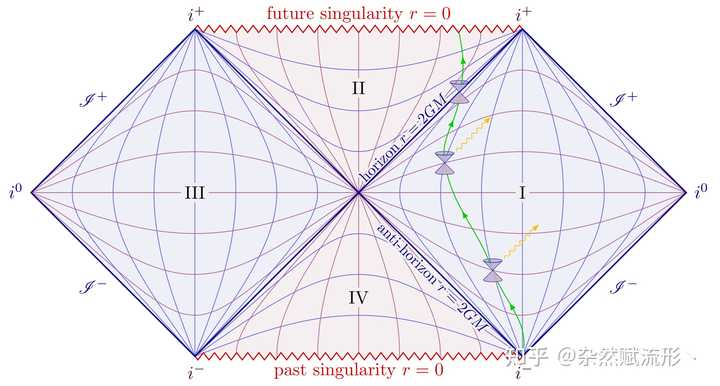
Bromwich 围道 由于题主问的是「酷炫」的图,我在网上也找到了一些示例作为补充。 因为代码太长比较占篇幅,建议去原网站 TikZ.net 和 TikZ-Gallery 里查询代码。 4. Penrose 图 |
|
|
彭罗斯图 1 |
|
|
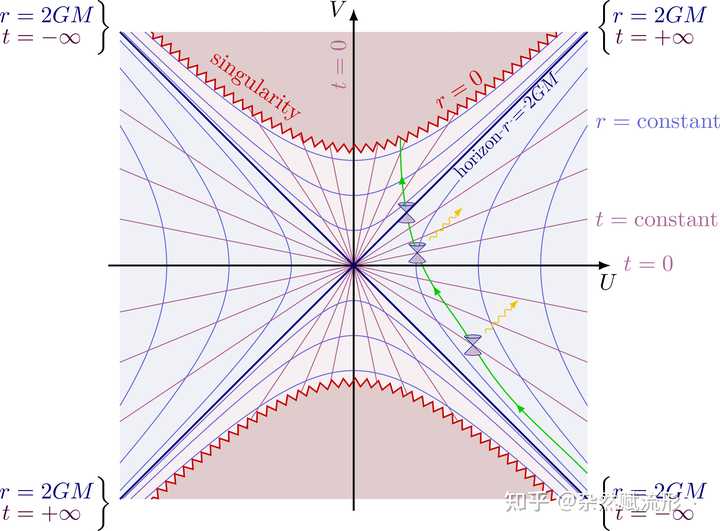
彭罗斯图 25. Kruskal 图 |
|
|
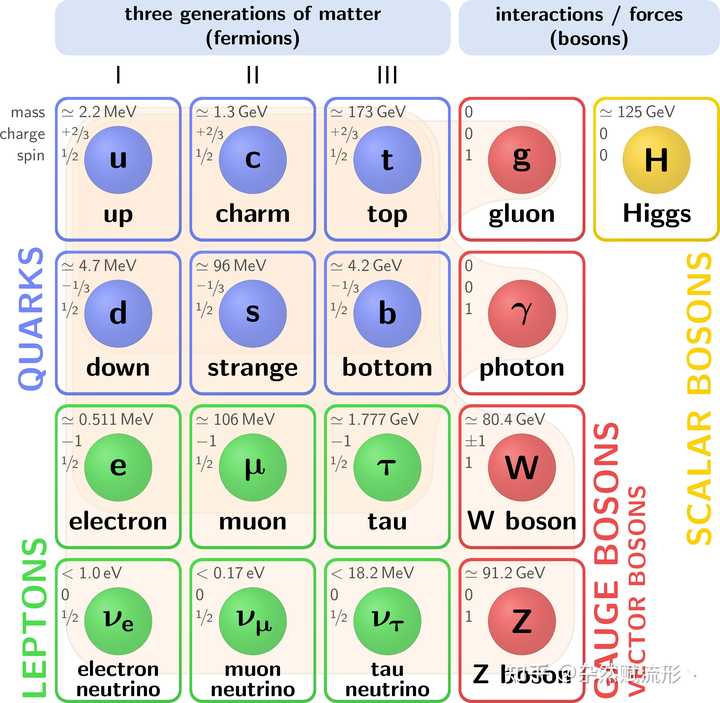
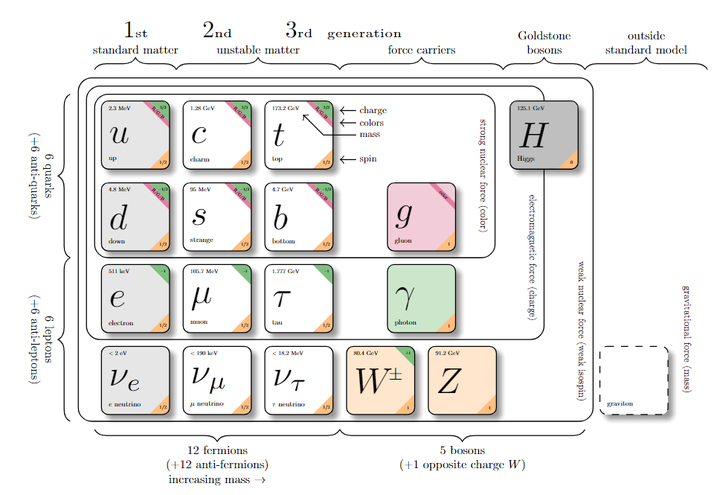
克鲁斯卡尔图6. 标准模型 |
|
|
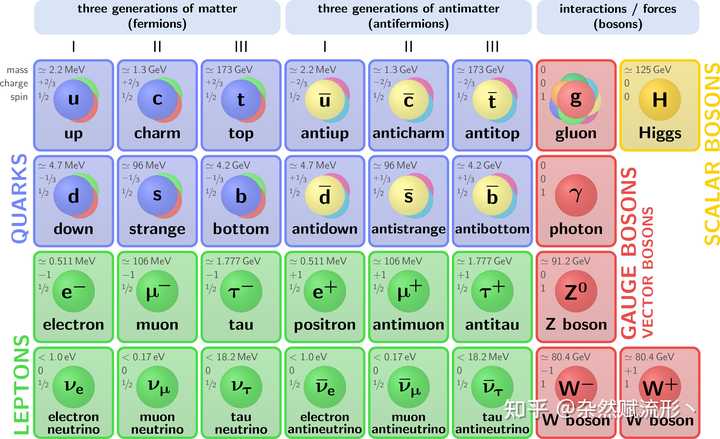
标准模型 1 |
|
|
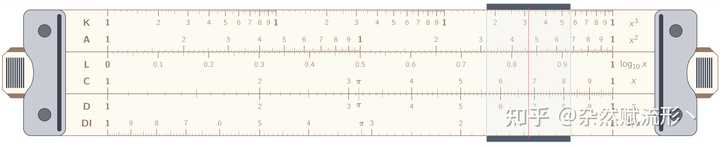
标准模型 27. 计算尺 |
|
|
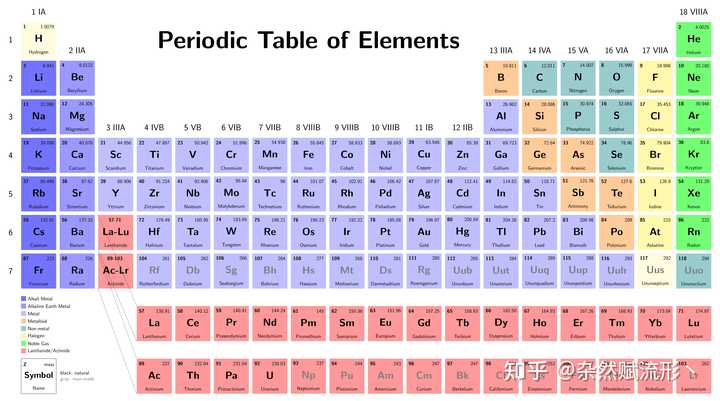
计算尺8. 元素周期表 |
|
|
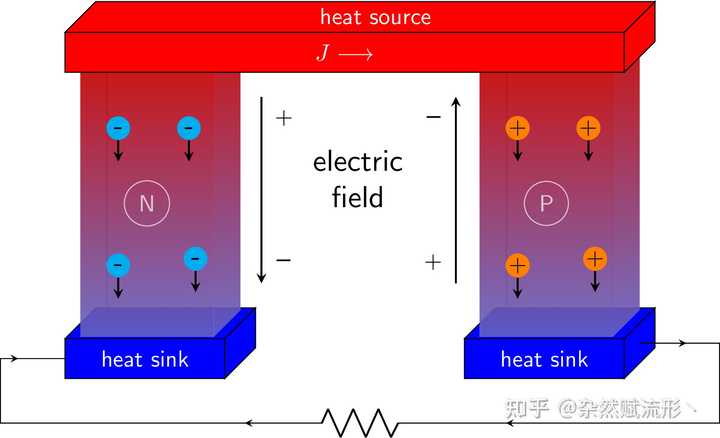
元素周期表9. Seebeck 效应 |
|
|
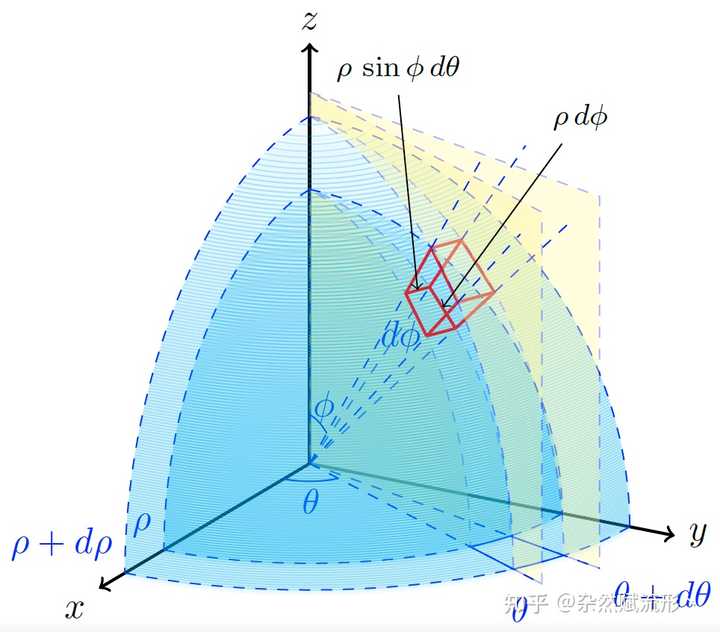
塞贝克效应10. 球坐标体积微元 |
|
|
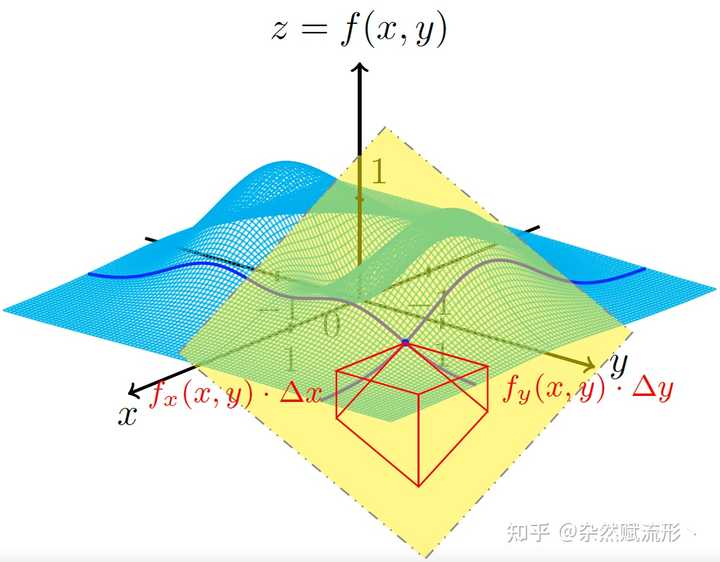
球坐标体积微元11. 三维空间中的线性近似 |
|
|
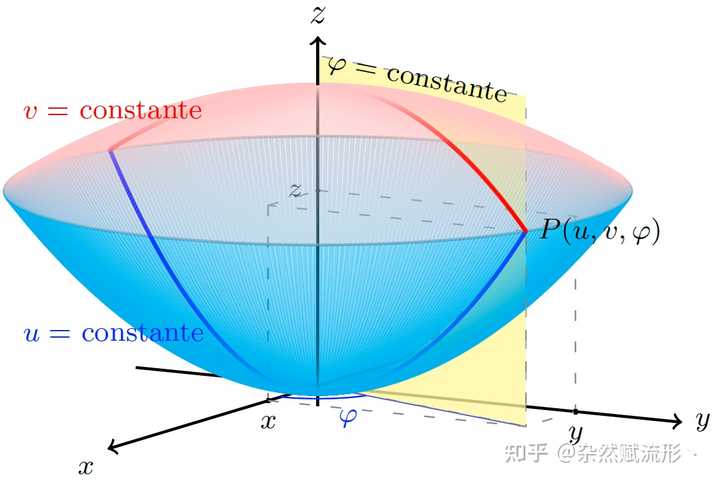
三维空间中的线性近似12. 抛物线坐标 |
|
|
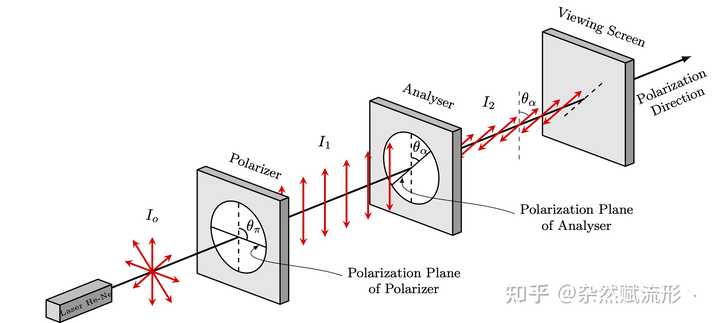
抛物线坐标13. 波片(相位延迟片) |
|
|
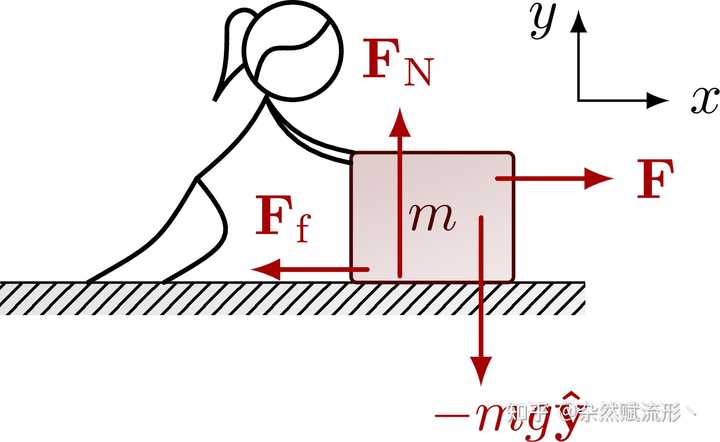
波片14. 受力分析 |
|
|
受力分析15. 费曼泰迪熊 |

|
|
用费曼图形式画出来的泰迪熊16. N 皇后问题 |
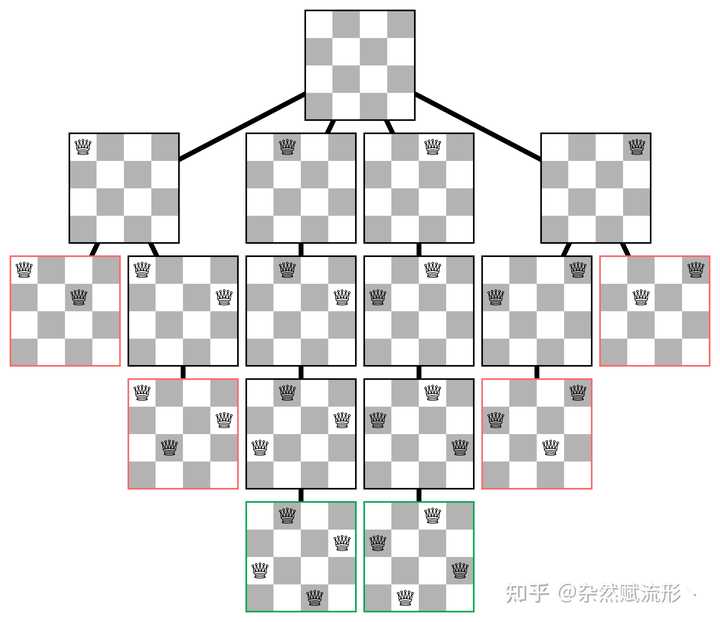
|
|
N 皇后问题17. 复杂网络 |
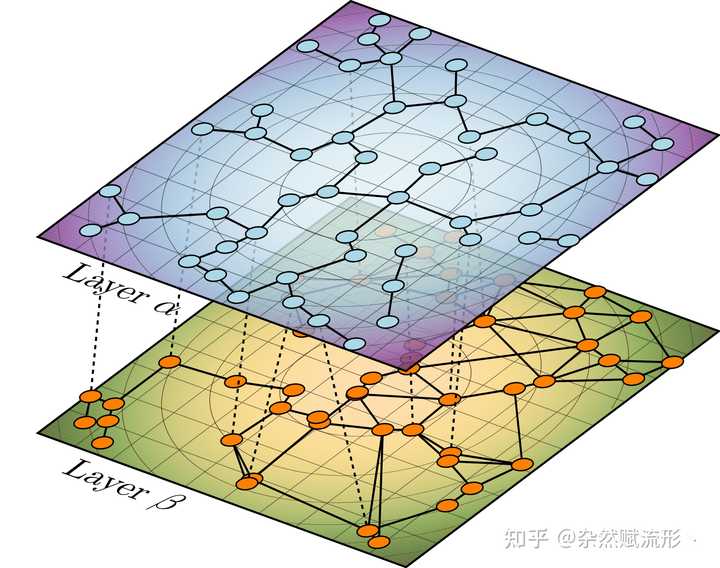
|
|
复杂网络18. 曼陀罗 |
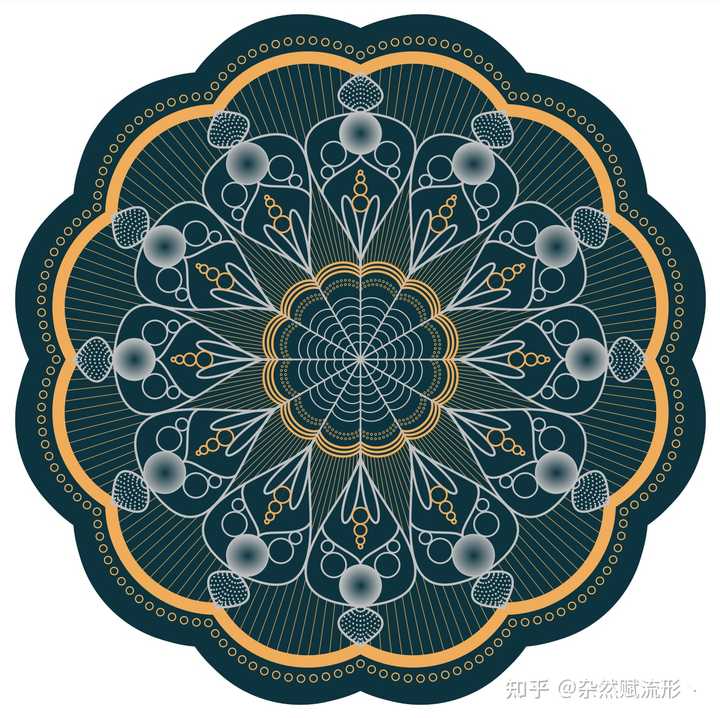
|
|
曼陀罗 |
|
自问自答,抛砖引玉. 参考: https://github.com/registor/awesome-TikZ-1?github.com/registor/awesome-TikZ-1 搬运: TeXample.net?texample.net/ smartdiagram 宏包 |
|
|
完全图 |
|
|
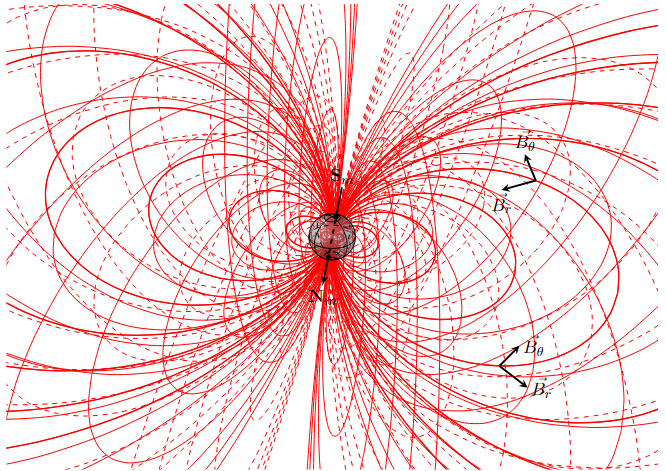
磁场 |
|
|
不可能三角形 |
|
|
Mandala |

|
|
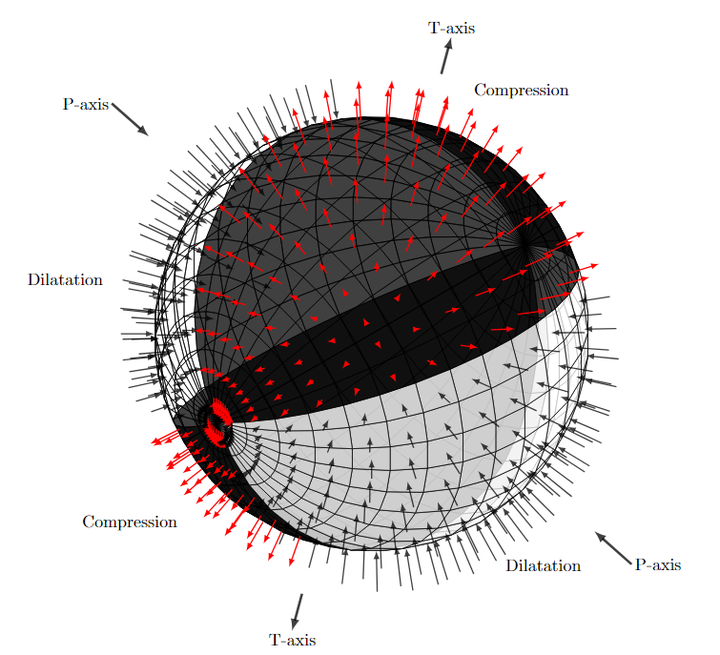
地震震源机制 |
|
|
旋转六边形 |

|
|
标准模型 |
|
|
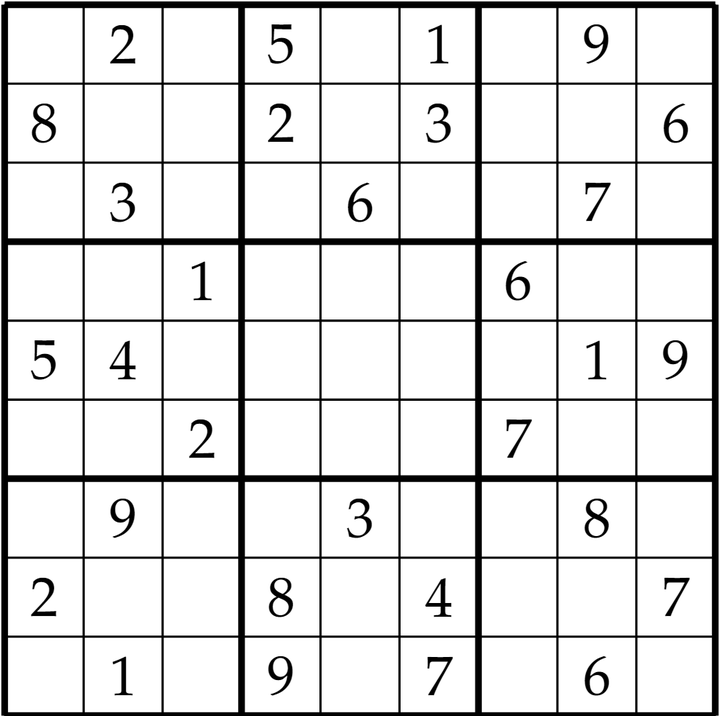
数独 |
|
|
|
|
知乎编辑器中绘制流程图和交换图做一个备忘。 不知道能不能绘制带拐弯的箭头和复杂的交换图。有知道的大佬可以指点一下。 1. 流程图绘制 其中我们使用语法 效果如下: a>> B \\ @VbVV @AAcA \\ C @= D \end{CD}\\">A→aBb↓↑cC=D" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">A→aBb↓↑cC=D\begin{CD} A @>a>> B \\ @VbVV @AAcA \\ C @= D \end{CD}\\ 应用上面语句可以尝试弄出一个化学反应的简单流程,如下: \ce{O2}>> \ce{NO} @>\ce{O2}>>\ce{NO2} @>\ce{H2O}>> \ce{HNO3} \end{CD}\\">NH3→O2NO→O2NO2→H2OHNO3" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">NH3→O2NO→O2NO2→H2OHNO3\begin{CD} \ce{NH3} @>\ce{O2}>> \ce{NO} @>\ce{O2}>>\ce{NO2} @>\ce{H2O}>> \ce{HNO3} \end{CD}\\ 再尝试一个稍微复杂的例子: \ce{O2}>> \ce{NO} @>\ce{O2}>>\ce{NO2} @>\ce{H2O}>> \ce{HNO3} \\ @.@A A\ce{O2}A\\ @.\ce{N2} \end{CD}\\">\begin{CD} \ce{NH3} @>\ce{O2}>> \ce{NO} @>\ce{O2}>>\ce{NO2} @>\ce{H2O}>> \ce{HNO3} \\ @.@A A\ce{O2}A\\ @.\ce{N2} \end{CD}\\ 流程图上面加上方框,用于试题的也能整出来了,代码如下: 效果如下: \ce{O2}>> \boxed{\ce{B}} @>\ce{O2}>>\boxed{\ce{C}} @>\ce{H2O}>> \boxed{\ce{D} } \\ @.@A A\ce{O2}A\\ @.\ce{X} \end{CD}\\">\begin{CD} @.@.Z\\ @.@.@VYVV\\ \boxed{\ce{A}} @>\ce{O2}>> \boxed{\ce{B}} @>\ce{O2}>>\boxed{\ce{C}} @>\ce{H2O}>> \boxed{\ce{D} } \\ @.@A A\ce{O2}A\\ @.\ce{X} \end{CD}\\ 2. 绘制交换图 首先定义一个代数系统 (A,*) ,即二元映射 * 满足封闭性: *:A\times A \rightarrow A\\ 2.1 交换律 设 \begin{array}{ccccc} \mathcal{Id}:& A\times A \rightarrow A\times A\\ &(x,y)\mapsto (x,y) \end{array} \\ \begin{array}{ccccc} \mathcal{E}:& A\times A \rightarrow A\times A\\ &(x,y)\mapsto (y,x) \end{array} \\ 则交换律等价于下面交换图 \mathcal{E}>> A\times A\\ @V*VV @VV*V\\ A@>\mathcal{Id}>> A \end{CD}\\">\begin{CD} A\times A@>\mathcal{E}>> A\times A\\ @V*VV @VV*V\\ A@>\mathcal{Id}>> A \end{CD}\\ 也就是说乘法运算 * 在对换变换下保持不变,这种对称性在列出乘法表时显得更加直观,所谓交换律,就是乘法表是一个关于主对角线对称的矩阵。 代码如下: 2.2 结合律 考虑乘法运算自身的「复合」: \begin{array}{ccccc} * \ \tilde{\circ} \ *:A\times A \rightarrow A\hookrightarrow A\times A \rightarrow A\\ (x,y)\mapsto (x*y,z) \mapsto (x*y)*z\end{array} \\ 或 * \ \tilde{\circ} \ *:A\times A\times A \rightarrow A\\ 设映射 \begin{array}{ccccc} \mathcal{F}:& A \times A \times A \rightarrow A\times A \times A\\ &(x,y,z)\mapsto (y,z,x) \end{array} \\ 则结合律等价于如下交换图: \mathcal{F}>> A\times A \times A @>* \ \tilde{\circ} \ \rm id >> A\times A @> \mathcal{E} >> A\times A\\ @V * \ \tilde{\circ} \ * VV&&&& @VV*V\\ A @>>> @>\mathcal{Id}>> @>>> A \end{CD}\\">\begin{CD} A\times A \times A @>\mathcal{F}>> A\times A \times A @>* \ \tilde{\circ} \ \rm id >> A\times A @> \mathcal{E} >> A\times A\\ @V * \ \tilde{\circ} \ * VV&&&& @VV*V\\ A @>>> @>\mathcal{Id}>> @>>> A \end{CD}\\ 也就是说乘法运算 * \ \tilde{\circ} \ * 在上述一系列变换下保持不变。 这里 \mathcal{E}, \mathcal{F}\in S_3 ,即可以视为3次对称群的元素,前者是 (12) 后者是 (132) 。 代码如下: 2.3 分配律 我们需要考虑两种运算 (A,+,*) ,分配律等价于下面是交换图: + \ \tilde{\circ} \ \rm id>> A \times A @>* >> A\\ @V\mathcal{D}VV&&& @VV\mathcal{Id}V\\ A\times A \times A \times A @>(*,*)>> A \times A @>+>> A \end{CD}\\">\begin{CD} A\times A \times A@>+ \ \tilde{\circ} \ \rm id>> A \times A @>* >> A\\ @V\mathcal{D}VV&&& @VV\mathcal{Id}V\\ A\times A \times A \times A @>(*,*)>> A \times A @>+>> A \end{CD}\\ 其中 \mathcal{D}: (x,y,z)\mapsto ((x,z),(y,z)) 代码如下: 3. 参考链接In order to use this environment you need to have the amscd package loaded which is done with the \usepackage{amscd} command that goes in the preamble. The environment is eclosed in \begin{CD} and \end{CD} end each row (except the last) with \\ "vertices of the diagram are refered to as "corners" above. a horizontal row arrow is produced with (i) @>>> or (ii) @> {...} >> or (iii) @>> {...} > depending on whether you want no label, a label above the arrow or below the arrow respectively. a vertical row arrow is produced with (i) @VVV or (ii) @V {...} VV or (iii) @VV {...} V depending on whether you want no label, a label to the left of the arrow or to the right of the arrow respectively. Sometimes a commutative diagram is triangular in which case we typeset a square diagram and use @= to indicate equality. Commutative diagrams do not have to have the same number of row as columns but they are on a rectangular grid. There are more complicated programs available for more sophisticated diagrams. If you include a label then you can cross-reference your diagram with the \label and \ref commands. 注意里边的代码(at符号和水平箭头和垂直箭头之间不能留空格): {f} >> {H} \\ @V{\phi} VV @VV {\psi} V \\ {X} @>> {T} > {Y} \\ \end{CD}\\">\begin{CD} {G} @> {f} >> {H} \\ @V{\phi} VV @VV {\psi} V \\ {X} @>> {T} > {Y} \\ \end{CD}\\ 效果如下: {上标签} >> {右上角标签} \\ @V{左标签} VV @VV {右标签} V \\ {左下角标签} @>> {下标签} > {右下角标签} \\ \end{CD}\\">\begin{CD}\label{} {左上角标签} @> {上标签} >> {右上角标签} \\ @V{左标签} VV @VV {右标签} V \\ {左下角标签} @>> {下标签} > {右下角标签} \\ \end{CD}\\ |
|
\LaTeX 色阶: $$\color{#ff0000}{\rule{0.1cm}{1cm}} \color{#ff0800}{\rule{0.1cm}{1cm}} \color{#ff1100}{\rule{0.1cm}{1cm}} \color{#ff1900}{\rule{0.1cm}{1cm}} \color{#ff2200}{\rule{0.1cm}{1cm}} \color{#ff2a00}{\rule{0.1cm}{1cm}} \color{#ff3300}{\rule{0.1cm}{1cm}} \color{#ff3c00}{\rule{0.1cm}{1cm}} \color{#ff4400}{\rule{0.1cm}{1cm}} \color{#ff4d00}{\rule{0.1cm}{1cm}} \color{#ff5500}{\rule{0.1cm}{1cm}} \color{#ff5e00}{\rule{0.1cm}{1cm}} \color{#ff6600}{\rule{0.1cm}{1cm}} \color{#ff6f00}{\rule{0.1cm}{1cm}} \color{#ff7800}{\rule{0.1cm}{1cm}} \color{#ff8000}{\rule{0.1cm}{1cm}} \color{#ff8900}{\rule{0.1cm}{1cm}} \color{#ff9100}{\rule{0.1cm}{1cm}} \color{#ff9a00}{\rule{0.1cm}{1cm}} \color{#ffa200}{\rule{0.1cm}{1cm}} \color{#ffab00}{\rule{0.1cm}{1cm}} \color{#ffb300}{\rule{0.1cm}{1cm}} \color{#ffbc00}{\rule{0.1cm}{1cm}} \color{#ffc500}{\rule{0.1cm}{1cm}} \color{#ffcd00}{\rule{0.1cm}{1cm}} \color{#ffd600}{\rule{0.1cm}{1cm}} \color{#ffde00}{\rule{0.1cm}{1cm}} \color{#ffe700}{\rule{0.1cm}{1cm}} \color{#fff000}{\rule{0.1cm}{1cm}} \color{#fff800}{\rule{0.1cm}{1cm}} \color{#fcff00}{\rule{0.1cm}{1cm}} \color{#f4ff00}{\rule{0.1cm}{1cm}} \color{#ebff00}{\rule{0.1cm}{1cm}} \color{#e3ff00}{\rule{0.1cm}{1cm}} \color{#daff00}{\rule{0.1cm}{1cm}} \color{#d2ff00}{\rule{0.1cm}{1cm}} \color{#c9ff00}{\rule{0.1cm}{1cm}} \color{#c0ff00}{\rule{0.1cm}{1cm}} \color{#b8ff00}{\rule{0.1cm}{1cm}} \color{#afff00}{\rule{0.1cm}{1cm}} \color{#a7ff00}{\rule{0.1cm}{1cm}} \color{#9eff00}{\rule{0.1cm}{1cm}} \color{#96ff00}{\rule{0.1cm}{1cm}} \color{#8dff00}{\rule{0.1cm}{1cm}} \color{#84ff00}{\rule{0.1cm}{1cm}} \color{#7cff00}{\rule{0.1cm}{1cm}} \color{#73ff00}{\rule{0.1cm}{1cm}} \color{#6bff00}{\rule{0.1cm}{1cm}} \color{#62ff00}{\rule{0.1cm}{1cm}} \color{#5aff00}{\rule{0.1cm}{1cm}} \color{#51ff00}{\rule{0.1cm}{1cm}} \color{#48ff00}{\rule{0.1cm}{1cm}} \color{#40ff00}{\rule{0.1cm}{1cm}} \color{#37ff00}{\rule{0.1cm}{1cm}} \color{#2fff00}{\rule{0.1cm}{1cm}} \color{#26ff00}{\rule{0.1cm}{1cm}} \color{#1eff00}{\rule{0.1cm}{1cm}} \color{#15ff00}{\rule{0.1cm}{1cm}} \color{#0cff00}{\rule{0.1cm}{1cm}} \color{#04ff00}{\rule{0.1cm}{1cm}} \color{#00ff04}{\rule{0.1cm}{1cm}} \color{#00ff0c}{\rule{0.1cm}{1cm}} \color{#00ff15}{\rule{0.1cm}{1cm}} \color{#00ff1d}{\rule{0.1cm}{1cm}} \color{#00ff26}{\rule{0.1cm}{1cm}} \color{#00ff2f}{\rule{0.1cm}{1cm}} \color{#00ff37}{\rule{0.1cm}{1cm}} \color{#00ff40}{\rule{0.1cm}{1cm}} \color{#00ff48}{\rule{0.1cm}{1cm}} \color{#00ff51}{\rule{0.1cm}{1cm}} \color{#00ff5a}{\rule{0.1cm}{1cm}} \color{#00ff62}{\rule{0.1cm}{1cm}} \color{#00ff6b}{\rule{0.1cm}{1cm}} \color{#00ff73}{\rule{0.1cm}{1cm}} \color{#00ff7c}{\rule{0.1cm}{1cm}} \color{#00ff84}{\rule{0.1cm}{1cm}} \color{#00ff8d}{\rule{0.1cm}{1cm}} \color{#00ff96}{\rule{0.1cm}{1cm}} \color{#00ff9e}{\rule{0.1cm}{1cm}} \color{#00ffa7}{\rule{0.1cm}{1cm}} \color{#00ffaf}{\rule{0.1cm}{1cm}} \color{#00ffb8}{\rule{0.1cm}{1cm}} \color{#00ffc0}{\rule{0.1cm}{1cm}} \color{#00ffc9}{\rule{0.1cm}{1cm}} \color{#00ffd1}{\rule{0.1cm}{1cm}} \color{#00ffda}{\rule{0.1cm}{1cm}} \color{#00ffe3}{\rule{0.1cm}{1cm}} \color{#00ffeb}{\rule{0.1cm}{1cm}} \color{#00fff4}{\rule{0.1cm}{1cm}} \color{#00fffc}{\rule{0.1cm}{1cm}} \color{#00f8ff}{\rule{0.1cm}{1cm}} \color{#00f0ff}{\rule{0.1cm}{1cm}} \color{#00e7ff}{\rule{0.1cm}{1cm}} \color{#00deff}{\rule{0.1cm}{1cm}} \color{#00d6ff}{\rule{0.1cm}{1cm}} \color{#00cdff}{\rule{0.1cm}{1cm}} \color{#00c5ff}{\rule{0.1cm}{1cm}} \color{#00bcff}{\rule{0.1cm}{1cm}} \color{#00b4ff}{\rule{0.1cm}{1cm}} \color{#00abff}{\rule{0.1cm}{1cm}} \color{#00a2ff}{\rule{0.1cm}{1cm}} \color{#009aff}{\rule{0.1cm}{1cm}} \color{#0091ff}{\rule{0.1cm}{1cm}} \color{#0089ff}{\rule{0.1cm}{1cm}} \color{#0080ff}{\rule{0.1cm}{1cm}} \color{#0078ff}{\rule{0.1cm}{1cm}} \color{#006fff}{\rule{0.1cm}{1cm}} \color{#0066ff}{\rule{0.1cm}{1cm}} \color{#005eff}{\rule{0.1cm}{1cm}} \color{#0055ff}{\rule{0.1cm}{1cm}} \color{#004dff}{\rule{0.1cm}{1cm}} \color{#0044ff}{\rule{0.1cm}{1cm}} \color{#003cff}{\rule{0.1cm}{1cm}} \color{#0033ff}{\rule{0.1cm}{1cm}} \color{#002aff}{\rule{0.1cm}{1cm}} \color{#0022ff}{\rule{0.1cm}{1cm}} \color{#0019ff}{\rule{0.1cm}{1cm}} \color{#0011ff}{\rule{0.1cm}{1cm}} \color{#0008ff}{\rule{0.1cm}{1cm}} \color{#0000ff}{\rule{0.1cm}{1cm}} \color{#0000ff}{\rule{0.1cm}{1cm}} \\$$ |
|
回忆我在 tex-sx 上看到的、印象深刻的绘图, 一个是高度对称的几何图案,因其设计性和对称性。伊斯兰几何图案是其中的一类,已有回答举例。另一个(一类)是阴影/渐变/shading/fading 团,因为它们像是横跨了矢量和点阵绘图的边界,或者说,难复刻。它们依然是「矢量」的,放大并不会变模糊,PDF 阅读器会根据函数重新计算每个点的颜色。贴到知乎的自然只能是点阵的。 曼陀罗花,出自 tex-sx 用户 Mark Wibrow 2019 年的回答https://tex.stackexchange.com/a/496442" data-tooltip-richtext="1" data-tooltip-preset="white" data-tooltip-classname="ztext-reference-tooltip">[1] |

|
|
平行光下的球,出自 tex-sx 用户 Simon Byrne 2012 年的回答https://tex.stackexchange.com/a/75994" data-tooltip-richtext="1" data-tooltip-preset="white" data-tooltip-classname="ztext-reference-tooltip">[2] |

|
|
高阶高斯光束(Gaussian beamhttps://en.wikipedia.org/wiki/Gaussian_beam#Higher-order_modes" data-tooltip-richtext="1" data-tooltip-preset="white" data-tooltip-classname="ztext-reference-tooltip">[3];我不懂其中的物理意义,只是翻译了名词),出自 tex-sx 用户 Symbol 1 的两个回答https://tex.stackexchange.com/a/333409" data-tooltip-richtext="1" data-tooltip-preset="white" data-tooltip-classname="ztext-reference-tooltip">[4]https://tex.stackexchange.com/a/476275" data-tooltip-richtext="1" data-tooltip-preset="white" data-tooltip-classname="ztext-reference-tooltip">[5],分别对应 Hermite-Gaussian modes 和 Laguerre-Gaussian modes。 |

|
|
Hermite-Gaussian modes |

|
|
Laguerre-Gaussian modes 上述精细的渐变图,都是通过 tikz 的 \pgfdeclarefunctionalshading 直接向 PDF 写入使用 PostScript 数学函数的式子得到的。tikz 文档里明确提示, Warning: These shadings are the least portable of all and they put the heaviest burden of the renderer. They are slow and, possibly, will not print correctly! 备注 在不介意炫技的前提下,例如要为 ctexbook 制作扉页上的图案,那么你会想用 LaTeX 本身绘制什么美丽或酷炫的图形? 抱歉只侧重了问题标题里的「炫酷」,忽略了问题描述里的「为 ctexbook 制作扉页上的图案」。 参考^https://tex.stackexchange.com/a/496442^https://tex.stackexchange.com/a/75994^https://en.wikipedia.org/wiki/Gaussian_beam#Higher-order_modes^https://tex.stackexchange.com/a/333409^https://tex.stackexchange.com/a/476275 |
|
|
| [收藏本文] 【下载本文】 |
| 明星艺术 最新文章 |
| 入坑了,出不来了,有没有人再推荐点你会主 |
| 哪一句相声台词让你难忘? |
| 如何评价希特勒的绘画水平? |
| 你能用徒手画出一个多么有趣的马? |
| 你认为央视春晚历史上的最佳小品是哪个? |
| 如何评价苑琼丹? |
| 喜剧之王赵本山资产十辈子花不完,徒弟们整 |
| 敢不敢留下一张自拍照让人打分? |
| 曹云金巡演票价这么低,主办方能赚到钱吗? |
| 为什么现在的建筑不盖成古代那样了? |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
|
古典名著
名著精选
外国名著
儿童童话
武侠小说
名人传记
学习励志
诗词散文
经典故事
其它杂谈
小说文学 恐怖推理 感情生活 瓶邪 原创小说 小说 故事 鬼故事 微小说 文学 耽美 师生 内向 成功 潇湘溪苑 旧巷笙歌 花千骨 剑来 万相之王 深空彼岸 浅浅寂寞 yy小说吧 穿越小说 校园小说 武侠小说 言情小说 玄幻小说 经典语录 三国演义 西游记 红楼梦 水浒传 古诗 易经 后宫 鼠猫 美文 坏蛋 对联 读后感 文字吧 武动乾坤 遮天 凡人修仙传 吞噬星空 盗墓笔记 斗破苍穹 绝世唐门 龙王传说 诛仙 庶女有毒 哈利波特 雪中悍刀行 知否知否应是绿肥红瘦 极品家丁 龙族 玄界之门 莽荒纪 全职高手 心理罪 校花的贴身高手 美人为馅 三体 我欲封天 少年王 旧巷笙歌 花千骨 剑来 万相之王 深空彼岸 天阿降临 重生唐三 最强狂兵 邻家天使大人把我变成废人这事 顶级弃少 大奉打更人 剑道第一仙 一剑独尊 剑仙在此 渡劫之王 第九特区 不败战神 星门 圣墟 |
|
|
| 网站联系: qq:121756557 email:121756557@qq.com |