[明星艺术] 「数学之美」有什么例子？

阅读网购物网址万年历小说 | 三丰软件天天财富小游戏

TxT小说阅读器
↓小说语音阅读,小说下载↓

一键清除系统垃圾
↓轻轻一点,清除系统垃圾↓

图片批量下载器
↓批量下载图片,美女图库↓

图片自动播放器
↓图片自动播放,产品展示↓

佛经: 故事佛经佛经精华心经金刚经楞伽经南怀瑾星云法师弘一大师名人学佛佛教知识标签

名著: 古典现代外国儿童武侠传记励志诗词故事杂谈道德经讲解词句大全词句标签哲理句子

网络: 舞文弄墨恐怖推理感情生活潇湘溪苑瓶邪原创小说故事鬼故事微小说耽美师生内向易经后宫鼠猫美文

教育信息历史人文明星艺术人物音乐影视娱乐游戏动漫 | 穿越校园武侠言情玄幻经典语录三国演义西游记红楼梦水浒传

阅读网 -> 明星艺术 -> 「数学之美」有什么例子？ -> 正文阅读

[明星艺术]「数学之美」有什么例子？

[收藏本文] 【下载本文】

最好能够举出例子。尤其是那些高深一点的数学。

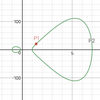
几何+数论？
几何背景下的数论问题：
存在边长和面积都是整数的非直角三角形吗？
{a=p2−q2+r2−s2b=p2+q2c=r2+s2S=pq(p2−q2+r2−s2)" role="presentation">{a=p2?q2+r2?s2b=p2+q2c=r2+s2S=pq(p2?q2+r2?s2)\begin{cases} a=p^2-q^2+r^2-s^2\\b=p^2+q^2\\c=r^2+s^2\\S=pq(p^2-q^2+r^2-s^2)\end{cases}
其中 pq=rs" role="presentation">pq=rspq=rs
比如 p=3,q=4,r=2,s=6" role="presentation">p=3,q=4,r=2,s=6p=3,q=4,r=2,s=6
显然这样的三角形有无穷多个。
存在两个边长都是整数，且周长和面积都是对应相等的整数的的三角形吗？
{a=24b=37c=37S=420C=98" role="presentation">{a=24b=37c=37S=420C=98\begin{cases} a=24\\b=37\\c=37\\S=420\\C=98\end{cases}
{a=25b=34c=39S=420C=980" role="presentation">{a=25b=34c=39S=420C=980\begin{cases} a=25\\b=34\\c=39\\S=420\\C=980\end{cases}
2001年，Mohammed Aassila证明了这样的三角形对有无穷多对。
存在三个边长都是整数且周长和面积都对应相等的的三角形吗？
{a=24b=37c=37S=420C=98" role="presentation">{a=24b=37c=37S=420C=98\begin{cases} a=24\\b=37\\c=37\\S=420\\C=98\end{cases}
{a=25b=34c=39S=420C=98" role="presentation">{a=25b=34c=39S=420C=98\begin{cases} a=25\\b=34\\c=39\\S=420\\C=98\end{cases}
{a=29b=29c=40S=420C=98" role="presentation">{a=29b=29c=40S=420C=98\begin{cases} a=29\\b=29\\c=40\\S=420\\C=98\end{cases}
2004年，Ronald van Luijk证明了存在这样的任意数量为一组的三角形。
存在边长和面积都是整数，且边长成等差数列的三角形吗？
{a=3p2+3q2b=6p2+2q2c=9p2+q2S=6pq(3p2+q2)" role="presentation">{a=3p2+3q2b=6p2+2q2c=9p2+q2S=6pq(3p2+q2)\begin{cases} a=3p^2+3q^2\\b=6p^2+2q^2\\c=9p^2+q^2\\S=6pq(3p^2+q^2)\end{cases}
存在边长、面积、各顶点到内切圆圆心的距离都是整数的三角形吗？
设内切圆半径为 r" role="presentation">rr
{|AB|=r2−a22a+r2−b22b|BC|=(r2+b2)2(r2−a2)2bd|AC|=r2−a22a+2r2[(r2−a2)b2+(r2−b2)a2]dS=r(|AB|+|AC|+|BC|)2|OA|=r2+a22a|OB|=r2+b22b|OC|=r(r2+b2)(r2+a2)d" role="presentation">{|AB|=r2?a22a+r2?b22b|BC|=(r2+b2)2(r2?a2)2bd|AC|=r2?a22a+2r2[(r2?a2)b2+(r2?b2)a2]dS=r(|AB|+|AC|+|BC|)2|OA|=r2+a22a|OB|=r2+b22b|OC|=r(r2+b2)(r2+a2)d\begin{cases} |AB|=\frac{r^2-a^2}{2a}+\frac{r^2-b^2}{2b}\\|BC|=\frac{(r^2+b^2)^2(r^2-a^2)}{2bd}\\|AC|=\frac{r^2-a^2}{2a}+\frac{2r^2[(r^2-a^2)b^2+(r^2-b^2)a^2]}{d}\\S=\frac{r(|AB|+|AC|+|BC|)}{2}\\|OA|=\frac{r^2+a^2}{2a}\\|OB|=\frac{r^2+b^2}{2b}\\|OC|=\frac{r(r^2+b^2)(r^2+a^2)}{d}\end{cases}
其中 d=(r2−a2)(r2−b2)−4abr2" role="presentation">d=(r2?a2)(r2?b2)?4abr2d=(r^2-a^2)(r^2-b^2)-4abr^2
比如 a=16,b=18,r=72" role="presentation">a=16,b=18,r=72a=16,b=18,r=72
那么
{|AB|=289|BC|=231|AC|=250S=27720|OA|=170|OB|=153|OC|=120" role="presentation">{|AB|=289|BC|=231|AC|=250S=27720|OA|=170|OB|=153|OC|=120\begin{cases} |AB|=289\\|BC|=231\\|AC|=250\\S=27720\\|OA|=170\\|OB|=153\\|OC|=120\end{cases}
存在六条棱的长度、四个面的面积、四面体体积都是整数的四面体吗？
可以认为每条棱同时扩大整数 k" role="presentation">kk 倍后的四面体与原来的四面体是等价的，本质上是同一类四面体。
1992年，澳大利亚纽卡斯尔大学的R.H.Buchholz应用椭圆曲线的理论证明了互不等价的完美四面体有无穷多个[1]，
而且指出最长棱最小的这样的三棱锥（四面体）A−BCD" role="presentation">A?BCDA-BCD 的六条棱长是：
|AB|=51,|AC|=52,|AD|=84|BC|=53,|CD|=80,|BD|=117" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">|AB|=51,|AC|=52,|AD|=84|BC|=53,|CD|=80,|BD|=117|AB|=51,|AC|=52,|AD|=84\\|BC|=53,|CD|=80,|BD|=117\\ SΔABC=1170,SΔACD=2016,SΔABD=1890,SΔBCD=1800" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">SΔABC=1170,SΔACD=2016,SΔABD=1890,SΔBCD=1800S_{\Delta ABC}=1170,S_{\Delta ACD}=2016,\\S_{\Delta ABD}=1890,S_{\Delta BCD}=1800\\ VA−BCD=18144" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">VA?BCD=18144V_{A-BCD}=18144\\

Buchholz, R. (1992). Perfect pyramids. Bulletin of the Australian Mathematical Society, 45(3), 353-368. doi:10.1017/S0004972700030252
是否存在各棱长，面积和体积都是整数的四面体??www.zhihu.com/question/616384504/answer/3158163510?utm_psn=1750624524519989248

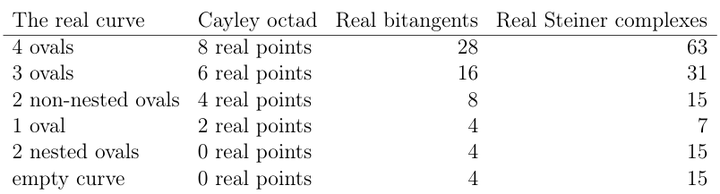
几何+代数？
使用解析几何，射影几何等方法研究代数曲线：
一个关于双切线的经典结果：射影空间中光滑的 d" role="presentation">dd 次非退化代数曲线上的双切线数量是 12d(d−2)(d2−9)" role="presentation">12d(d?2)(d2?9)\frac{1}{2}d(d-2)(d^2-9) ，显然 d≥4" role="presentation">d≥4d\geq 4 才有双切线。
定义在实数域上的光滑的四次非退化代数曲线上恰好包含4、8、16或者28条实的双切线（取决于曲线在实射影空间的拓扑）(1873,Zeuthen)。
在实射影空间的的光滑的四次代数曲线的6种拓扑类型

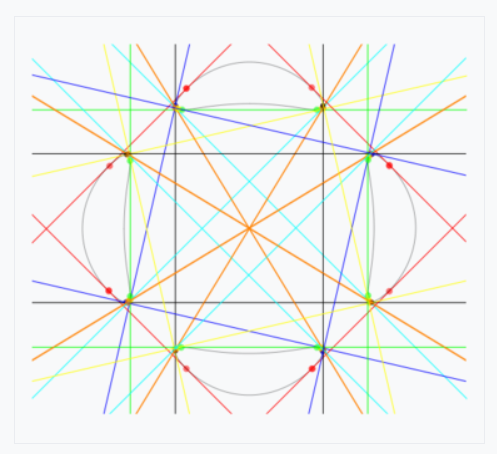
Daniel Plaumann, Bernd Sturmfels, and Cynthia Vinzant. Quartic curves and their bitangents
恰好包含28条实的双切线的光滑的四次代数曲线：
Trott曲线：
144(x4+y4)−225(x2+y2)+350x2y2+81=0" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">144(x4+y4)?225(x2+y2)+350x2y2+81=0\large 144(x^4+y^4)-225(x^2+y^2)+350x^2y^2+81=0\\

https://handwiki.org/wiki/Bitangents_of_a_quartic#/media/File:TrottCurveBiTangents7.svg

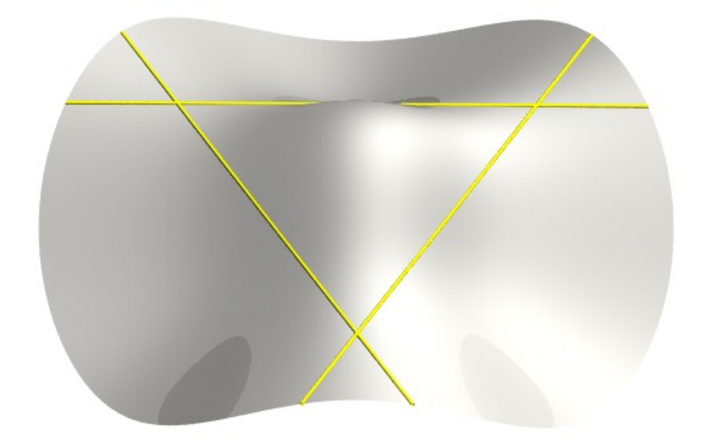
https://handwiki.org/wiki/Bitangents_of_a_quartic
1983年，中国数学家陆家羲在国际上发表了关于不相交斯坦纳三元系大集的系列论文，解决了国际上组合设计理论研究中多年未解决的难题，这项研究成果获得 1987 年中国自然科学界的最高荣誉—国家自然科学奖一等奖，其中涉及的“斯坦纳系列”就是瑞士数学家斯坦纳在研究四次曲线的二重切线时遇到的一种区组设计[2]。
定义在实数域上的光滑的三次非退化代数曲面上恰好包含3、7、15或者27条实直线。
①恰好包含3条实直线的三次光滑曲面：
x3+y3+z3=a3" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">x3+y3+z3=a3\large x^3+y^3+z^3=a^3\\

https://mathcurve.com/surfaces/cubic/cubic.shtml
②恰好包含7条实直线的三次光滑曲面：
xyz=a(x2+y2−z2)+a3" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">xyz=a(x2+y2?z2)+a3\large xyz=a(x^2+y^2-z^2)+a^3\\

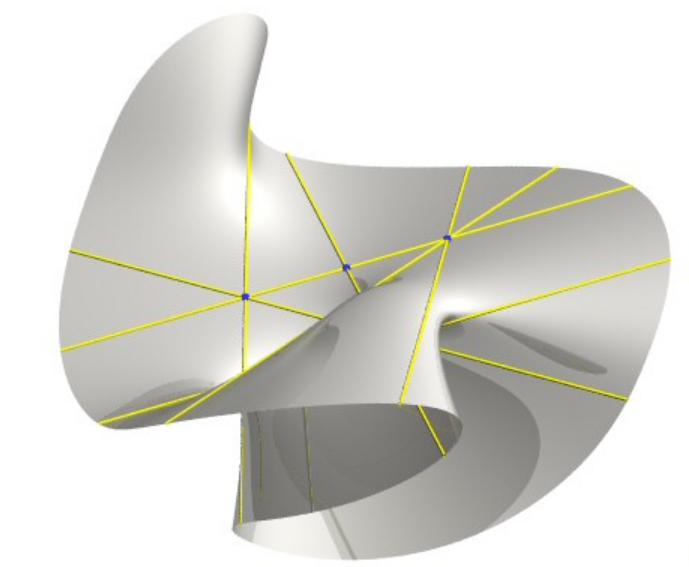
https://mathcurve.com/surfaces/cubic/cubic.shtml
③恰好包含15条实直线的三次光滑曲面：
z(z2−a2)=x(x2−3y2)" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">z(z2?a2)=x(x2?3y2)\large z(z^2-a^2)=x(x^2-3y^2)\\

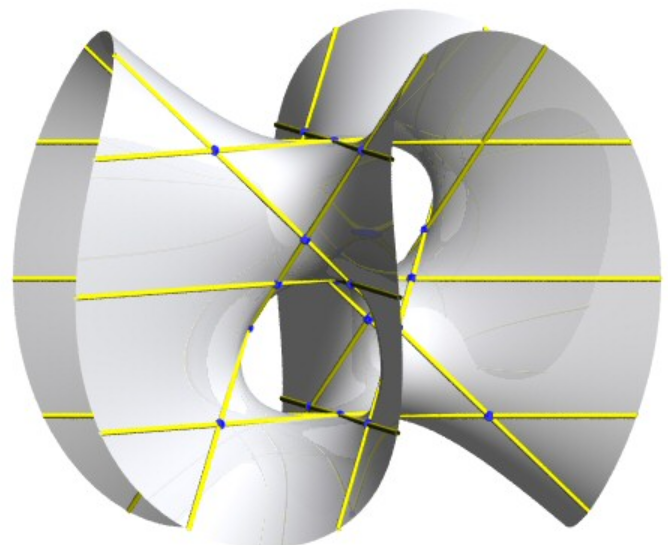
https://mathcurve.com/surfaces/cubic/cubic.shtml
④恰好包含27条实直线的三次光滑曲面：
Clebsch对角曲面。定义在复数域上的三次光滑曲面上恰好包含27条直线，这个曲面在复数域也没有多余的直线了。

https://mathcurve.com/surfaces/clebsch/clebsch.shtml
在谈及希尔伯特的第13个数学问题时，我们看到，在1927年，希尔伯特描述了一种新的技巧。他首先确定了所有可能的方法来简化九次多项式，并在其中发现了一族特殊的三次曲面。希尔伯特已经知道，每一个光滑的三次曲面，包含正好27条直线。他意识到，如果他知道其中的一条线，他就可以简化九次多项式，找到它的根。这个公式只需要四个参数，换句话说，这意味着解析度最多为4。希尔伯特把重点放在三次曲面上，以求解一个变量的九次多项式[3]。
实际上，一个光滑的平面四次代数曲线的28条双切线与一个光滑的三次代数曲面上的27条直线密切相关，它们以及亏格4的经典六次代数曲线的120个三切平面，Vladimir Arnold称之为“三元组”，是McKay对应关系的一种形式[4]。
数论+几何？
素数螺旋，也称乌拉姆螺旋（Ulam spiral）

https://baike.baidu.com/picture/3329096/3329096/0/3c2c4bfba81f44236c22eb3e#aid=1&pic=32fa828ba61ea8d37bf46dc1970a304e241f5824
脑筋急转弯＋图论？
一个猎人带着一只羊，一只狼和一棵白菜回家，路上遇到一条河。
河边只有一条船，但船太小，一次最多只可载猎人和另一样东西过河。
但猎人不在时，狼要吃羊，羊要吃白菜。
请问怎样才能把狼，羊，白菜都安全运过河?
河边一共只有十种状态是可以存在的，分别是人狼羊菜、人羊菜、人狼菜、人狼羊、狼菜、人羊、狼、羊、菜、空。
以每种状态作为一个顶点，状态之间如果可以转化，那么这两个状态对应的顶点之间连一条边
此题步骤最少的运法就是从“人狼羊菜”这个顶点到“空”这个顶点的一条最短路径。
此题的两个解是：

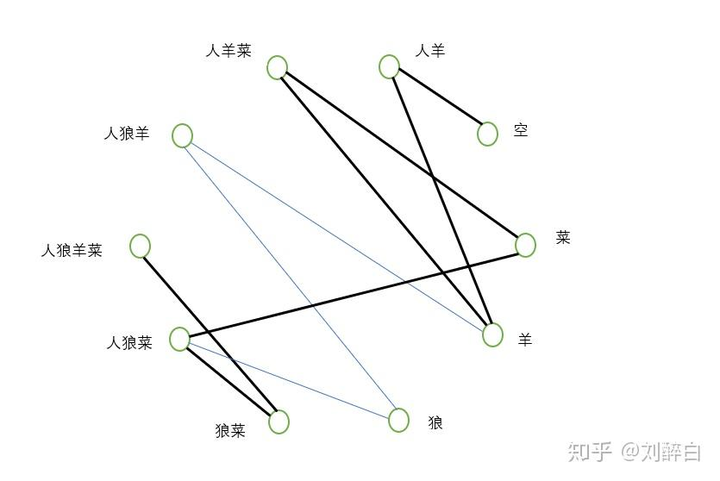
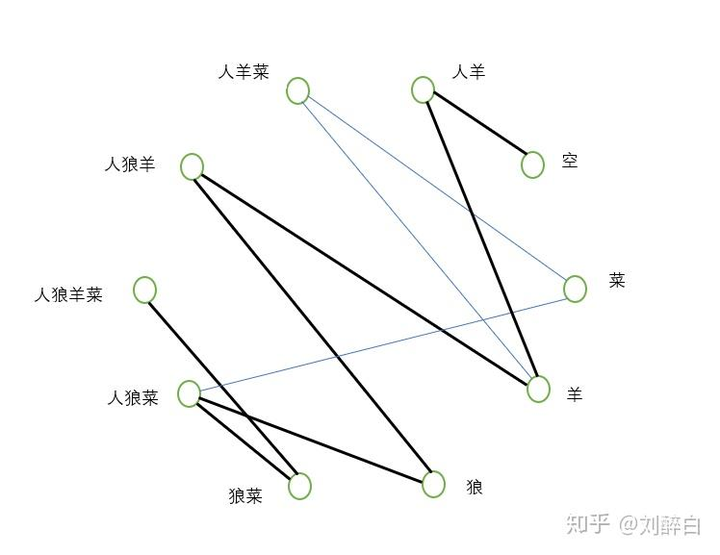
参考^Buchholz, R. (1992). Perfect pyramids. Bulletin of the Australian Mathematical Society, 45(3), 353-368. doi:10.1017/S0004972700030252^http://math0.bnu.edu.cn/~jgbao/xinxifabu/meitishuxue(200910-201009).pdf^https://zhuanlan.zhihu.com/p/345133339^https://handwiki.org/wiki/Bitangents_of_a_quartic

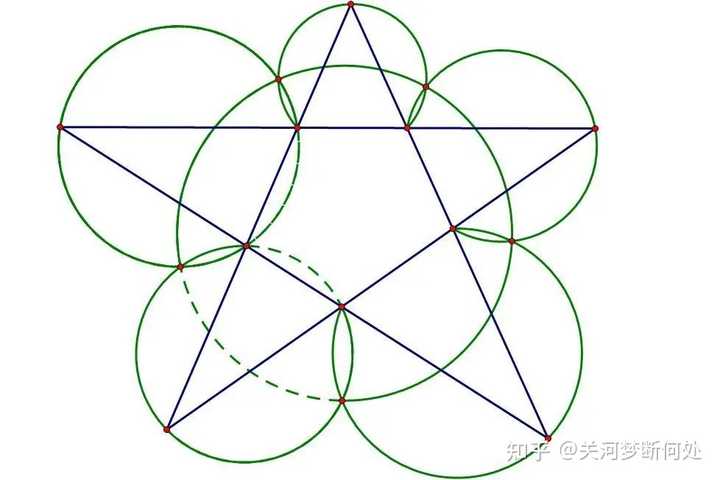
2000年12月20日，长者出席澳门回归祖国一周年庆典活动期间，在参观濠江中学时向该校师生出了一道求证“五点共圆”的平面几何题：“假设：任意一个星形，五个三角形，外接圆交于五点。求证：这五点共圆。”

我最为推崇暴力美学。没有什么是数值解决不了的。如果有，就多来几招。
1）如优化问题，最简单是所谓“梯度下降法”：
\begin{aligned} f^{\rm{new}}(x) =f^{\rm{old}}(x)- \gamma \left[\frac{\partial f(x)}{\partial x}\right ] \\ \end{aligned}
针对一个性质好的连续函数，可以找到其局域极小点。这招加上随机性，就是目前最热门的深度神经网络的最流行的优化方法：随机梯度下降。
2）还有求解常微分方程的“欧拉法”：
如果有一个常微分方程，
y'(t) \equiv \frac{{\rm{d}}y(t)}{{\rm{d}}t}= f(t,y(t))
它的解可以按照如下方法计算：
y_{n+1} = y_{n} + h f(t_n, y_n)
3) 中心差分法计算梯度：
\begin{aligned} \frac{\partial f(\boldsymbol{x})}{\partial x_i} & = \frac{f(x_1, x_2, \cdots, x_i +h, x_{i+1},\cdots) - f(x_1, x_2, \cdots, x_i -h, x_{i+1},\cdots)}{2h} \\ & \boldsymbol{x} = (x_1, x_2, \cdots, x_N) \end{aligned}
4) 梯形积分法：
\int f(x) {\rm{d}}x = \sum_{i=1}^{N-1}\frac{(f(x_i) +f(x_{i+1}))h }{2}
5）Monte Carlo法：
\begin{aligned} & {\rm{do\, \, utill\, \,}} i< N\\ & \quad \eta \in [0,1)\\ & \quad {\rm{if}}\, \, \eta< {\rm{Probability}}\\ & \quad \quad {\rm{Accept}}\\ & \quad {\rm{End\, \, if}}\\ & \quad i += 1\\ & {\rm{End\, \, do}} \\ \end{aligned}
6）最小二乘法：
设有一组数据点 \left\{x_i, y_i \right\}_{i=1}^{N} 找一条直线拟合这些数据：
y(x) = w x + b
那么有表达式：
w = \frac{{\rm{COVAR}[x,y]}}{{\rm{VAR}}[x]}
这里
{\rm{COVAR}} [x,y]=\frac{1}{N} \sum_{i=1}^{N}(x_i - {\rm{E}}[x])(y_i - {\rm{E}}[y])
{\rm{VAR}}[x] =\frac{1}{N} \sum_{i=1}^{N}(x_i - {\rm{E}}[x])^2
{\rm{E}}[x] =\frac{1}{N} \sum_{i=1}^{N}x_i
以上全都是最简单的数值计算方法，背后的数学推导也不复杂。但现代的机器学习方法都来源于这里。
关于矩阵计算，还有非常有趣的Gauss消元法、LU分解法、QR分解法、共轭梯度法等等。而矩阵本征值问题就更有趣，有所谓的Givens旋转法和Householder旋转法等等。矩阵计算还跟求解偏微分方程密切相关，如有限差分法。
求解积分还有一套非常神奇的方法：Gauss quadrature方法。采用有限的几个点，至多不超过20个点，就可以足够精确地计算积分！还可以求无穷积分如Gauss-Laguerre是求 [0, +\infty) 区间的积分，而Gauss-Hermite是求 (-\infty,\infty) 区间的积分的。
在使用上述方法的时候，我总是惊叹于前辈大数学家们能发明出这么多节省脑细胞的方法！

数学王子高斯

谢邀
说到数学之美的话，我个人的感受觉得应该需要满足两个方面：
1.形式之简单；
2.结论之深刻；
形式简单让人易于理解，结论深刻引人深思，好像最广为人知的应该就属费马大定理了吧，要说它，可以说上一整本书，所以我还是说点别的吧。
那么由这两点出发给例子的话，我马上能想到的有这些：
1.分形中的Mandelbrot set和Julia set

以上为Mandelbrot set的原始图像及放大图像。

此为C =（0.285, 0.01）时的Julia set。
如此绚丽的Mandelbrot set和Julia set其实仅仅是由如下一个非常简单的迭代生成的：
Z_{n+1}=Z_n^2+C
区别仅在于Mandelbrot set是由复平面上所有使得序列{Z_n}有限的点C组成，而Julia set是在固定C的前提下，所有使得序列{Z_n}有限的初值Z_0所组成的点。形式上的简单和美丽不言而喻。
而对于结论之深刻，分形属于混沌理论的一部分，在混沌理论中，有一个很有意思的定理，该定理叙述如下：
假设 f 是一个从实数到实数的连续映射，如果 f 有周期为3（即复合 f 三次回到自身，满足f(f(f(x)))=x的x）的点，则 f 有任意的周期点（即对于所有的正整数n， f 复合n次都有不动点）。
从叙述上我们简单的说这个定理说的就是“三生万物”，因此该定理的中文名就叫“三生混沌”（Period Three Implies Chaos）。从这个角度看数学定理中所蕴含的哲理也是实在太丰富了。
2.机械求积公式和共鸣定理
我们知道对于计算而言，到今天为止，我们所能够掌握的不过也还就是加减乘除而已，计算机虽然强大，其实说到底也就不过如此。但是工具虽简单，我们能做到的事却不简单，这就是数学许诺给我们的天堂。
所谓机械求积公式，是指如下的一种对积分的逼近：
\int_{a}^{b} f(x)dx\approx \sum_{k=1}^{n}{A_kf(x_k)}
其中x_k为区间[a,b]中的一些分点，而A_k为对应分点的权重系数，常用的梯形公式，simpson公式，gauss求积公式，都是它的特殊形式。可以看到右边的逼近仅仅就是加减乘除的近似，这也就是它的重要之处。
既然是逼近，那么最基本的问题就是当我们取的点足够多时，我们是否能得到那个等号，而这一点就被泛函分析中的共鸣定理所保证了。具体的我不阐述了，大家有兴趣可以google一下。
数学是严谨的，它用逻辑严格限定了我们所能做的，但它同时又是自由的，在规则之下，我们充分施展我们的想象，我们所能得到的即是真理。
3.巴拿赫-塔斯基定理
它的另一个名字可能更广为人知一些---分球定理，叙述如下：
这一定理指出在选择公理成立的情况下，可以将一个三维实心球分成有限（不可测的）部分，然后仅仅通过旋转和平移到其他地方重新组合，就可以组成两个半径和原来相同的完整的球。
简单的说就是可以无中生有。
我选择这个有点病态的例子的主要原因是我觉得这种逻辑的力量正是数学最强大的内涵，在承认某些基本事实的前提下，演绎推理，即使结论再古怪，我们也勇于承认它的正确性，实事求是不外乎如此。
最后总结一下，其实我觉得数学之美不仅仅是体现在理论方面理想化的用无穷描述这个复杂的世界，实际上我们也是在不断地在用真实可控的有限来逼近世界，改造世界，比如上面提到的第二个例子就是如此。恩，我想，世界应该就是这样收敛的。

1. 抽象。或者说，不断用简洁的语言去描述复杂的概念。
比如说，我们曾经在微积分的课程上研究过各种奇形怪状的函数，而在泛函分析理论中，所有的函数都抽象成了泛函空间中的“点”，于是我们可以轻松地定义点与点之间的距离，来描述两个不同函数之间的差异。
--------
在这个过程中，我们一下子上升到非常宏观的视角去看待世界，意识到原先的我们只不过是井底之蛙。这个成长的过程着实让人激动。（突然想到了“发现更大的世界”...）
2. 逻辑严密。
比方说关于“素数的个数无穷多”这个命题有一个经典的证明方法：假定素数只有有限个，令它们为p1, p2, ..., pn. 那么构造 P = p1 · p2 · ··· · pn + 1，它比所有素数都大，而且不能被任意一个已有素数整除，所以它是一个新的素数，与假设矛盾。
--------
有很多这样巧妙的证明都让我们陶醉在纯粹的思维过程带来的快乐中。
3. 形式上的美感。
第一次在数学教材上看到斯托克斯公式的这个形式时
\int_{\partial M}\omega = \int_{M}d\omega
我就有种被震撼到的感觉。
--------
即便不理解它的意思，这种简洁对称的符号表达有时候也会令人有所触动。（不过知乎的这个公式编辑器的效果貌似不如我在书上看到的漂亮。）
4. 干净纯粹。
这是我心目中数学最美的地方。数学让人觉得干净，原因之一是很多时候它没什么用，研究数学的人也不需要去考虑一个数学问题需要给社会带来什么实际的价值，甚至也不需要像物理化学那样关心实验的结果。这只是一个独立的王国，我们只需按照它的法则去享受游戏的过程就可以了。
曾经看到过一道号称名企面试题的题目：
1
11
21
1211
111221
312211
……
问序列的下一个数字串是什么。
看到答案后我几乎吐血了：第二行描述了第一行的构成：11可以理解为“1个1”，类似地，21表示2个1,1211表示1个2和1个1，以此类推，所以答案是13112221.
后来在一篇博客(http://www.matrix67.com/blog/archives/3870)上看到，这竟然还是一个很著名的序列，而且有些非常有趣的性质，譬如说数列中的数虽然会越来越长，但数字 4 始终不会出现；相邻两数的长度之比越来越接近一个常数等等。顿时觉得无比神奇。
--------
这个常数叫做Conway常数，是为了纪念发现他的数学家John Conway. 至少目前我完全没觉得发现这样一个结论有什么实际意义，不过即便是看到这个结论的我，也还是会像小时候发现了某个玩具时一样沉浸在非常单纯的快乐中。我觉得这就是数学最美好的地方。

[收藏本文] 【下载本文】

明星艺术最新文章

加:2024-03-15 12:04:37 更:2024-03-15 12:06:49

古典名著名著精选外国名著儿童童话武侠小说名人传记学习励志诗词散文经典故事其它杂谈
小说文学恐怖推理感情生活瓶邪原创小说小说故事鬼故事微小说文学耽美师生内向成功潇湘溪苑
旧巷笙歌花千骨剑来万相之王深空彼岸浅浅寂寞 yy小说吧穿越小说校园小说武侠小说言情小说玄幻小说经典语录三国演义西游记红楼梦水浒传古诗易经后宫鼠猫美文坏蛋对联读后感文字吧武动乾坤遮天凡人修仙传吞噬星空盗墓笔记斗破苍穹绝世唐门龙王传说诛仙庶女有毒哈利波特雪中悍刀行知否知否应是绿肥红瘦极品家丁龙族玄界之门莽荒纪全职高手心理罪校花的贴身高手美人为馅三体我欲封天少年王
旧巷笙歌花千骨剑来万相之王深空彼岸天阿降临重生唐三最强狂兵邻家天使大人把我变成废人这事顶级弃少大奉打更人剑道第一仙一剑独尊剑仙在此渡劫之王第九特区不败战神星门圣墟

网站联系: qq:121756557 email:121756557@qq.com 阅读网