| |
|
| 阅读网 -> 教育信息 -> 考研名师汤家凤免单数学题出了个送分题却难倒众人遭吐槽,其回应称「怎么还有脸笑」,题目难度究竟有多大? -> 正文阅读 |
|
|
[教育信息]考研名师汤家凤免单数学题出了个送分题却难倒众人遭吐槽,其回应称「怎么还有脸笑」,题目难度究竟有多大? |
| [收藏本文] 【下载本文】 |
|
5月6日,知名考研数学教师汤家凤受邀为淘宝免单出了一道数学题,难倒了不少网友。 据媒体报道,其中有的大学生甚至还给十年没联系的数学老师打了电话,抱怨汤… |
|
对于考研的同学,这个确实是「送分题」 三个答案分别为1;1;0。第一个是三角函数变换中的万能公式;第二个e^x的泰勒展开公式;第三个是第一类重要极限。 |

|
|
不过,怎么说呢?对于常年不接触数学,外加没上过大学的人来说,这些题确实超纲了。你要知道,淘宝上专门去抢单的人,不会做的还挺多的。 你要知道,虽然都调侃“大学生遍地走”,但也并非所有大学生都会做的。 更何况,淘宝抢单的,很多还是五六十岁的妈妈阿姨辈,你让她们做,能做出就见鬼了。 都说“买菜用不到数学”,这回淘宝抢单可算是碰到数学题了,勾起了一些同学被数学题支配的恐惧。 当然了,也不要紧。不会的话,万能的网友早就做出答案,告诉你了,也不影响你抢单。重点还是抢单的手速。 淘宝和考研名师汤家凤合作,让老汤来出题,本身就是一次互利共赢的营销活动。为什么这么说?因为涉及到数学题,再简单也肯定有一堆人不会。 |

|
|
再加上汤家凤本身考研名师的流量,“你怎么睡得着觉”的经典片段太出名了,基本上很容易就能上热搜,哪怕一时半儿上不了,稍微推广一下就能冲榜。 就汤家凤老师本身来说, 曾几何时,考研数学一度是张宇、汤家凤争霸,现在武忠祥老师,外加李林的图书,还有后起的周洋鑫、杨超等人,老汤这几年,在考研数学的地位,已经非以往能比了。 我也希望汤老师,可以更加专注于教学,打磨一下1800的习题册,更上一层楼。 |

|
|
|
|
对他来讲确实是送分题。 看得出来是放了海了,大概率就是例题或者经典款题目改的,或者干脆就是某个特定结论。 比如第二题,虽然我现在记不太清,不过看上去就应该是泰勒级数经典款,但凡听课应该就知道,忘了的话查查资料应该就知道了。 但是说实在的,给网友看确实是有点难为人了。 毕竟一般人,说泰勒级数他都不知道是啥,你让做高数例题也是有点过分的。 |
|
既『高中概率语文化[1]』后,汤家凤老师又开创了『高等数学完形化』这一新型命题方式。 难度说实话没到大学,就是高考级别。 第一个考的是万能公式,高一学的;第二个看起来考的是泰勒展开,但高三基本上也会教一些『切线放缩』技巧;第三个考的是重要极限,这都是标准的高三内容。 ps说实话第三题我还真思考了会,主要是真没看到那个 ?" role="presentation">?\color{red}? 在什么地方。。。谁会想到居然在 lim" role="presentation">lim\lim 下面藏了个 ?" role="presentation">?\color{red} ? 啊。。。 关于评论区表示高中没教过这些内容的统一update:明确的讲,第一和第三题都是明确高中考纲要求的内容,都可以直接在考纲内找到对应的内容;对于第二,高中考纲中确实不会讲泰勒展开,但实际上高中导数题型中经常涉及的『切线放缩』之类的方式的本质就是泰勒展开,一般情况下也会补充一些相关的知识点。 高考考纲[2]里面涉及第一和第三如下: 『万能公式』的高考考纲要求 第一个是『万能公式』,这算比较常用的说法;实际上就是考纲中写的『二倍角的正切公式』。 |

|
|
不要认为这里有个半角就是那个不要求记忆的半角公式。半角公式是这个 tanθ2=1−cos⁡θsin⁡θ" role="presentation">tanθ2=1?cos?θsin?θ\tan \displaystyle \frac{\theta}2 =\displaystyle \frac{1-\cos \theta}{\sin \theta } 这个数学不要求,但是高中物理喜欢考,比如Archimon:精讲狂做1 单摆与等效重力法 重要极限的高考考纲相关内容 高中数学对于极限较为回避,但是讲导数不可能不涉及极限。 第三个是重要极限,但实际上高中教导数的时候都会提一下初等范围内的推导。 |
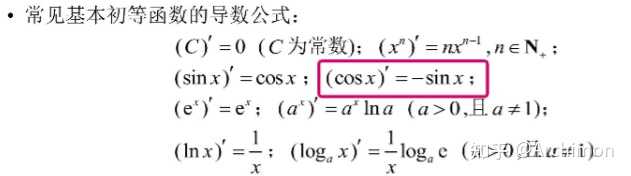
|
|
在教正弦函数的导数推导的时候就会提到这个极限了。 limΔx→0sin⁡(x+Δx)−sin⁡xΔx⇔limΔx→0sin⁡(x+12Δx+12Δx)−sin⁡((x+12Δx−12Δx)Δx⇔limΔx→0cos⁡(x+12Δx)limΔx→0sin⁡(12Δx)12Δx" role="presentation">limΔx→0sin?(x+Δx)?sin?xΔx?limΔx→0sin?(x+12Δx+12Δx)?sin?((x+12Δx?12Δx)Δx?limΔx→0cos?(x+12Δx)limΔx→0sin?(12Δx)12Δx\begin{aligned} \lim_{\Delta x \to 0}&\frac{\sin (x+\Delta x)-\sin x}{\Delta x} \\ \Leftrightarrow \lim_{\Delta x \to 0}&\frac{\sin (\color{green}{x+\displaystyle \frac 1 2\Delta x} +\color{purple}{\displaystyle\frac 1 2\Delta x})-\sin ((\color{green}{x+\displaystyle \frac 1 2\Delta x}-\color{purple}{\displaystyle \frac 1 2\Delta x})}{\Delta x} \\ \Leftrightarrow \lim_{\Delta x \to 0}&\cos\color{green}{(x+\displaystyle \frac 1 2\Delta x)} \lim_{\Delta x\to 0}\frac{\sin(\color{purple}{\displaystyle \frac 1 2\Delta x})}{\color{purple}{\displaystyle \frac 1 2\Delta x}} \\ \end{aligned} 对于上式绿色的部分,根据函数的连续性,可以比较自然地得 limΔx→0cos⁡(x+12Δx)=cos⁡x" role="presentation">limΔx→0cos?(x+12Δx)=cos?x\displaystyle \lim_{\Delta x\to0} \cos (x+\displaystyle \frac 1 2\Delta x ) = \cos x 而上式中的紫色部分,高中的数学老师一般就会简单地介绍一下这个重要极限 limx→0sin⁡(12Δx)12Δx=1" role="presentation">limx→0sin?(12Δx)12Δx=1\displaystyle \lim_{x\to 0}\frac{\sin(\color{purple}{\displaystyle \frac 1 2 \Delta x})}{\color{purple}{\displaystyle \frac 1 2\Delta x}} = 1 也就是本题里面考察的 limx→0sin⁡ΔxΔx=1" role="presentation">limx→0sin?ΔxΔx=1\displaystyle \lim_{x\to \color{red}{0}}\frac{\sin \Delta x}{\Delta x} = 1 至于第二个,高中范围内不教泰勒展开。但是会教一点简单的等价无穷小。。。或者说叫『常见大小关系』,抑或着叫『切线放缩法』之类东西,讲得内容都是下面这些: x→0,ex−1≥x≥ln⁡(x+1)" role="presentation">x→0,ex?1≥x≥ln?(x+1)x \to 0, \mathrm e^x -1 \ge x \ge \ln(x+1) 这些东西可以处理一些简单的导数放缩,算是导数大题的基础了。 参考^参见 https://www.zhihu.com/question/354904752/answer/3481202473^2019年普通高等学校招生全国统一考试大纲(理科数学) https://gaokao.neea.edu.cn/html1/report/19012/5965-1.htm |
|
我也分享三道送分题,汤家凤不一定能答出来。一、在一辆汽车的仪表盘上发现的,类似有机玻璃,这是干嘛的? |

|
|
答:这是红绿灯查看器,如果你排在第一个的话,这个东西能帮你反射头顶的光,你就能知道现在是什么灯了。二、办公楼旁边挖了一些随机的,不平行的沟,这是干嘛的? |

|
|
答:这是“评估试验性挖沟”,确保这片地下没有文物。三、在一座建筑的大门两侧发现了这样的锥形铁器,这是干嘛的? |

|
|
答:这是个套盖,来你家的客人可以用它熄灭火把。 你知道哪些有趣却无用的冷知识?1363 关注 · 211 回答问题 |
|
您别说,因为很多人对数学概念的学习都是依赖图形视觉的,也就是说依赖符号本身的写法,背的那些范式甚至傀儡变量名改一下都不会用 比如 0, \exists h>0, \forall \delta: |\mu-\delta|∀f>0,∃h>0,∀δ:|μ−δ|<h→|ε(δ)−x|<f" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">?f>0,?h>0,?δ:|μ?δ|<h→|ε(δ)?x|<f\lim_{h\to \mu}\varepsilon(h)=x\\ 大家想想看。再进一步,我们知道 ∀x(x∈A→p(x))⟺¬∃x(x∈A∧¬p(x))" role="presentation">?x(x∈A→p(x))???x(x∈A∧?p(x))\forall x (x \in A \to p(x)) \iff \lnot\exists x(x \in A \land \lnot p(x)) ,再进一步令 Σ(a,b)" role="presentation">Σ(a,b)\Sigma(a,b) 是一种服从半正定性、对称性、三角不等式的广义距离函数,那么还能更野一点,写成 0 \left(\not \exists x> 0 \left[\not \exists \varepsilon \left\{\Sigma\left(\varepsilon, f\right) \le x \land \Sigma\left(\delta\left(\varepsilon\right),\mu\right)\ge h\right\}^\phantom2\right]^\phantom2\right)\\">∄h>0(∄x>0[∄ε{Σ(ε,f)≤x∧Σ(δ(ε),μ)≥h}2]2)" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">?h>0(?x>0[?ε{Σ(ε,f)≤x∧Σ(δ(ε),μ)≥h}2]2)\not\exists h > 0 \left(\not \exists x> 0 \left[\not \exists \varepsilon \left\{\Sigma\left(\varepsilon, f\right) \le x \land \Sigma\left(\delta\left(\varepsilon\right),\mu\right)\ge h\right\}^\phantom2\right]^\phantom2\right)\\猜猜看对应的极限式又是什么。 然后到头来,在三角函数、求和号中间加各种商标、大头,就会因为不是 x" role="presentation">xx 而众人甚至都看不懂,遂被难倒 所以该题的区分度在于对于符号的熟悉。 |
|
人逼急了可什么事都干得出来, 除了数学题。 实事求是的说,作为一个文科生,又是一个法学博士生, 从高考开始到现在就没碰过数学了。 这都十多年过去了,我来逛个淘宝开心一下,没想到眼前一黑,突然悲从中来。 这三道题,我应该是就认识一个tan,cos和sin。 我知道这个是三角函数。 我知道有一个是求什么什么极限。 啪,就这么多,没了。 大家对法学院的误解有很多,但是据我了解,我们学院里头,很多人的数学都非常一般,因为数学和逻辑不一样,法律讲究的所谓的“逻辑思维”,和数学的学习,可能有所区别。 而且数学的这个“数”,有的人是天生没有的,就是老师说的“没有数感”。 我尤其记得高考完之后填志愿,专门找的是不要学数学的学科。 因此,我来到了法学院,我开始和文字打交道,看到数学都绕道走。 现在网购都方便了,买个菜都不用算数了,碰到活动凑满减的时候,系统购物车里头会自动计算平均单件的价格。 天知道这个功能多么有用!简直是数学无能患者的小救星! 所以,你要说做数学题,我和我的博士班同学们,大家怕是都卧龙凤雏。 以后这个数学题,我是辅导不了娃做了。 再不怕大家笑话的说一句, 这题我其实都看不懂…… 只能感慨一下:现代学科的分工其实很明确的,张三学科分管这个,李四学科分管那个。 如果不是真的有意识的“接触”数学,或者说,本学科之外的任何一个其他学科,那拿到题目,一脸懵是一种常态。 求求考研名师饶了我, 送分题我也是,真的,不会做啊! 逼急了啥都能做,除了数学题。 这数学题啊,哎,真是做不了啊。 (背手叹气) |
|
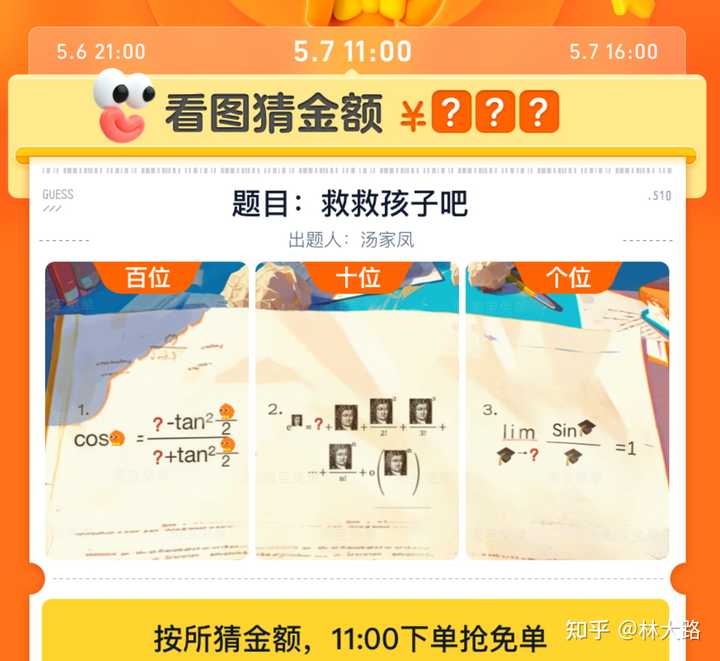
这个对于考研的人来说刚学过,已经学得很会了,确实是送分题,但是工作了10年的普通人一看: |
|
|
救救孩子?真的得救救孩子了,这完全是送命题了。 它都不是你拿个火柴棍就能算出来的东西,如果你忘记了这些你压根都不会读题,一脸懵逼。 人家上个淘宝,结果直接送命,而淘宝居然也真敢上这种题? 当然,你说这个题做对了直接免单1000元人民币的购物车,也行,立马全网薅羊毛去了。 但是你说这个做出来就两块八毛钱,那真的口吐芬芳了。你想引流回流搞免单都没有问题,但是这就属于恶心人了,真的是慢走不送。 |
|
那不得不先寄出支配了一代代数学考研学子的神图! |

|
|
|

|
|
言归正传,作为经过汤家凤老师洗礼过的考研老萌新,不敢说数学学的有多好,起码能看懂题。有幸运气上了个研究生。 回头看看这道题!我只能说!过于惊人! 我敢说只要学过数学半个月,喔不对,保守点,学过数学半年的人。 这些题目都是属于基础题。 第一题是三角函数变换、第二题是泰勒展开、第三题是极限, 汤神人家说的也没错啊,一眼出答案的东西,真心不难啊! |

|
|
不过,汤家凤老师出的题目的难度评价为简单,这个评价标准是面向学过数学的专业群体的。如果没接触过大学数学,其实可能真的连题目都看不懂 这汤老师受邀为淘宝免单出了一道数学题,更多的网友可能并没有学过高数,更别说专业课数学分析和高等代数等课程了,所以大部分网友应该是不会的。 这个就是现状。 如果出题改为出初高中的数学题,那大部分人都会做(高估本届网友的情况下),那也就失去了淘宝面单的意义(抄答案谁不会?) |

|
|
|

|
|
所以总结来说,题目对于学过数学的专业群体是送分题,对没学过数学的人来说是送命题。 而送分题群体人数较少,可能只占个10%,剩下90%都是送命题群体,、 那么,自然吐槽就成为了主流声音。 这一块,汤老师得吃一堑长一智啊,毕竟大部分网友真的没学过数学,而且应用场景还是在淘宝!当然会免单的人最后还是会。 |

|
|
|
|
文科毕业快20年,目前认真学习小学三年级课题,已经提前教会闺女入门三角函数的入门勾股定理。 第一题是有关三角函数的,答案是多少,按照经验是大概是1,我来讲讲我为什么这样认为。 首先呢,这个数字必须是整数,否则兑换不了钱。 cosX=(1+tan2X)/(1-tan2X) 然后就到了经验时刻。 -tan2x=tan2X 于是答案只存在1的可能,于是cosX=1 因为cos0?=1 tan0?=0 所以,我猜的答案是1,鱼是0度。 第二题我看看。 不会。 第三题我也不会。 |
|
对于研究生、准研究生来说,这个送分题的难度大抵是—— |

|
|
对于普通用户来说,难度大约是—— |

|
|
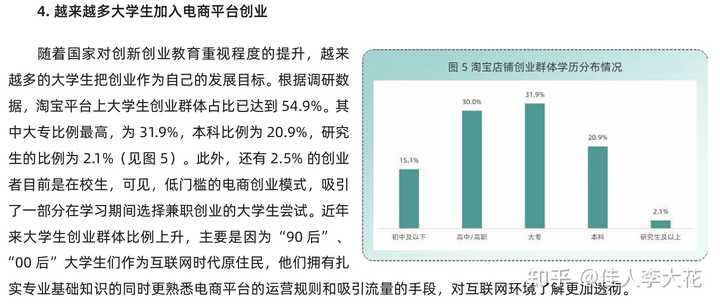
淘宝用户的学历分布无从调查,毕竟谁也不会买个东西还要先报上自己的学历…… 不过根据《2022电商平台大学生就业创业研究报告》统计的创业者学历分布,可以看到,虽然本科以上学历人群的数量有所增加,但仍是创业者中的“少数派”,研究生及以上只占到2.1%: |
|
|
也就是说,这道所谓的“送分题”,未必能有10%的卖家做出来,更何况数量更为庞大的买家群体。 而且,买东西的目的,一来是购置生活必需品,二来是花自己赚的钱,哄自己开心。 平台搞点活动,是为了让用户更开心,而不是为了恶心用户,让用户买点东西的同时,还要认识到自己知识储备的不足,承认自己技不如人,活该抢不到买单。 反正看到这个新闻,我是很无语,特意去问了问我妈的看法,她老人家的意见是“啥玩意?抽个免单还要做数学题??还是考研数学题??去TM的,我还不如去某多多上买呢,人家又便宜也不会耍我玩!” 所以,用户流失,被其他平台各种反超,恐怕都是“有迹可循”的。和自己请来的“嘉宾”一起鄙视嘲笑自己的用户,我是不太理解这套操作的。 如果这个免单题特指免单考研数学辅导教材,那我觉得还稍微可以理解一些…… |
|
学数学很容易遗忘,但以上三者可能是你为数不多能留在脑海中的数学痕迹。 三角函数常用恒等式,高一下学期的二倍角公式中的一个。 指数函数泰勒展开式,最基本的五个泰勒级数展开式之一。 两个重要极限之一,作为高等数学第一章的两个求解极限的基本例题之一。 这三道题不是会不会的问题,而是知不知道的问题。 因为你让一个学过高数的同学举出一个对微积分认识的实例,可能90%的人都会拿最后一道题的极限作为例子,因为其他微积分的东西他可能真的不记得了…… |
|
到卖课卖书办班的时候啦,没有争议怎么上热搜。 这些人本质上和张雪峰区别不大,生意的事非往学问上靠。 本事上,他们这些人都行,谁的理解明白都行,不是谁的价卖得高,谁会营销谁的就好,都差不多。 |
|
有些基础的人都能秒出答案,但真要一丝不苟的推导出来,还是有点难度的,尤其是后两道题。 |
|
简单,这些题我高中的时候就会做了。 第一道题,万能公式,高中拓展知识(做题从来没用过) 第二道题,指数函数泰勒展开,高中比大小题目可以用 第三道题,重要极限,自己高二网课的时候自学高数学过了。网课那会儿不想听数学课,就把高数上的第一章极限和第二章导数给学了 |
|
这个汤老师有点可爱 这又又上热搜啦? 我就感觉匪夷所思啊! |

|
|
表情1 你怎么睡的着的? |

|
|
表情2 这次多来一个:还有脸笑,你们怎么笑得出来? (表情在哪?) |

|
|
表情三 对于考研er,我建议别浪费汤老师的表情包啊! 除了上他的课,也或者不一定用他的课(毕竟每个老师上课风格不同,不是适合所有人),但是可以用他的表情包! 就贴在某处,比较显眼的地方就行啦。 (表情动动手指翻回去复习打印!) 每当复盘简单题,居然丢分了,居然丢分了,居然丢分了.... 我强烈建议你使用上面的图1表情: (配字幕:)我就感觉匪夷所思啊! 也或者用:还有脸笑,你们怎么笑得出来? 每当做一道题没有思路,抓头挠腮一无所获的时候! 每当做一道题,你明明知道可以一题多解,就是想不出来的时候 强烈建议用图3表情: (配字幕:)我有100种方法做这道题,而你无可奈何! (表情动动手指翻回去复习打印!) 每当你学了一会就想偷懒睡觉,就是游戏吃鸡喝农药的时候 想想汤老师,赶紧看看图2表情: (配字幕:)你怎么睡的着的?? (表情动动手指翻回去复习打印!) 没办法,只能牺牲牺牲汤老师了! 这回答权当是让考研er放松放松啦! 但我可不只是来搞笑的,毕竟俺也是带过不少学生的好吧,俺也是专业的好吧,更多精品内容可以参考往期关于考研的精品回答分享。 比如下面这些: 虽然是科目不是数学...但考研规划和英语复习、面试指导有问题的话还是可以找我聊聊的: 最后祝各位考研生,一“赞”上岸啦! 我是花生哥 教育价值分享者! 主要分享中高考、考研技巧和职场防坑资讯 专注有缘人 锁定和关注 @花生哥聊升学规划频道 升学规划不迷茫 人生规划更顺畅 只说大实话 一篇一干货 伴你成功路! |
|
|
| [收藏本文] 【下载本文】 |
| 教育信息 最新文章 |
| 大学里真的会有女生穿超短裙上课吗? |
| 为什么总说中国高中生辛苦,但是对他们收获 |
| 如何看待牢A在2月15日直播中提出的留学策略 |
| 如何看待「不要完全相信老师的话,他们是社 |
| 怎样看最近牢a在直播中呼吁留学生把外国教授 |
| 网传北科、北交、北林、地大 2027 年起启用 |
| 大学宿舍毁了多少人? |
| 计算机科学领域有什么笑话? |
| 老实人被逼急了会怎么样呢? |
| 经济学博士,除了当老师,还有什么好去处么 |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
|
古典名著
名著精选
外国名著
儿童童话
武侠小说
名人传记
学习励志
诗词散文
经典故事
其它杂谈
小说文学 恐怖推理 感情生活 瓶邪 原创小说 小说 故事 鬼故事 微小说 文学 耽美 师生 内向 成功 潇湘溪苑 旧巷笙歌 花千骨 剑来 万相之王 深空彼岸 浅浅寂寞 yy小说吧 穿越小说 校园小说 武侠小说 言情小说 玄幻小说 经典语录 三国演义 西游记 红楼梦 水浒传 古诗 易经 后宫 鼠猫 美文 坏蛋 对联 读后感 文字吧 武动乾坤 遮天 凡人修仙传 吞噬星空 盗墓笔记 斗破苍穹 绝世唐门 龙王传说 诛仙 庶女有毒 哈利波特 雪中悍刀行 知否知否应是绿肥红瘦 极品家丁 龙族 玄界之门 莽荒纪 全职高手 心理罪 校花的贴身高手 美人为馅 三体 我欲封天 少年王 旧巷笙歌 花千骨 剑来 万相之王 深空彼岸 天阿降临 重生唐三 最强狂兵 邻家天使大人把我变成废人这事 顶级弃少 大奉打更人 剑道第一仙 一剑独尊 剑仙在此 渡劫之王 第九特区 不败战神 星门 圣墟 |
|
|
| 网站联系: qq:121756557 email:121756557@qq.com |